Correlation Coefficients#

from datascience import *
from cs104 import *
import numpy as np
%matplotlib inline

1. Finch data#

# Load finch data 
finch_1975 = Table().read_table("data/finch_beaks_1975.csv")
finch_1975.show(6)

species	Beak length, mm	Beak depth, mm
fortis	9.4	8
fortis	9.2	8.3
scandens	13.9	8.4
scandens	14	8.8
scandens	12.9	8.4
fortis	9.5	7.5

... (400 rows omitted)

fortis = finch_1975.where('species', 'fortis')
fortis.num_rows

scandens = finch_1975.where('species', 'scandens')
scandens.num_rows

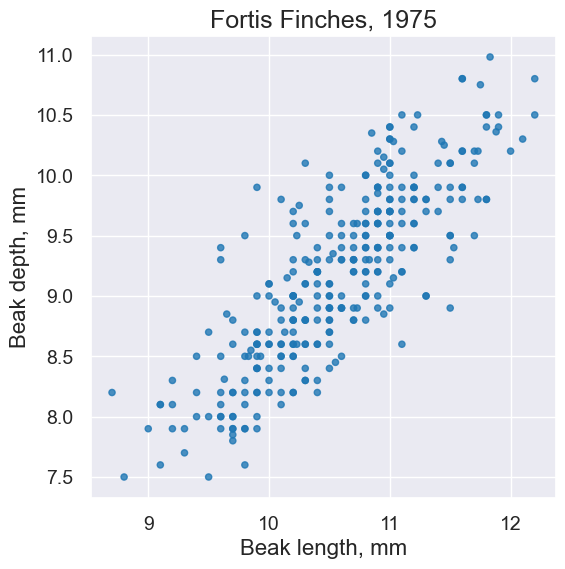
plot = fortis.scatter('Beak length, mm', 'Beak depth, mm')
plot.set_title('Fortis Finches, 1975')

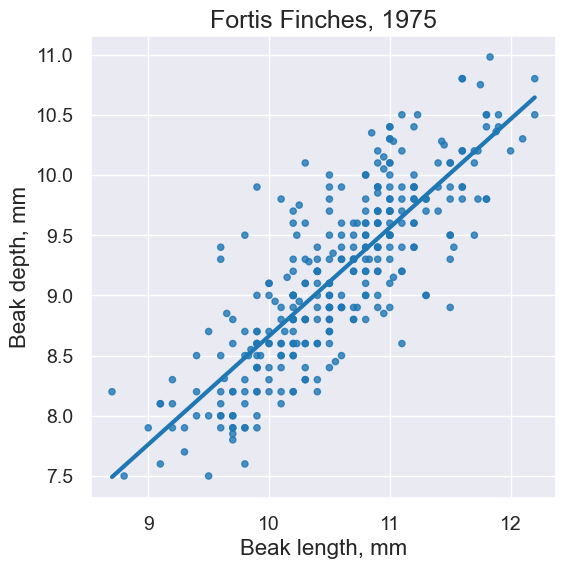
plot = fortis.scatter('Beak length, mm', 'Beak depth, mm', fit_line=True)
plot.set_title('Fortis Finches, 1975') 

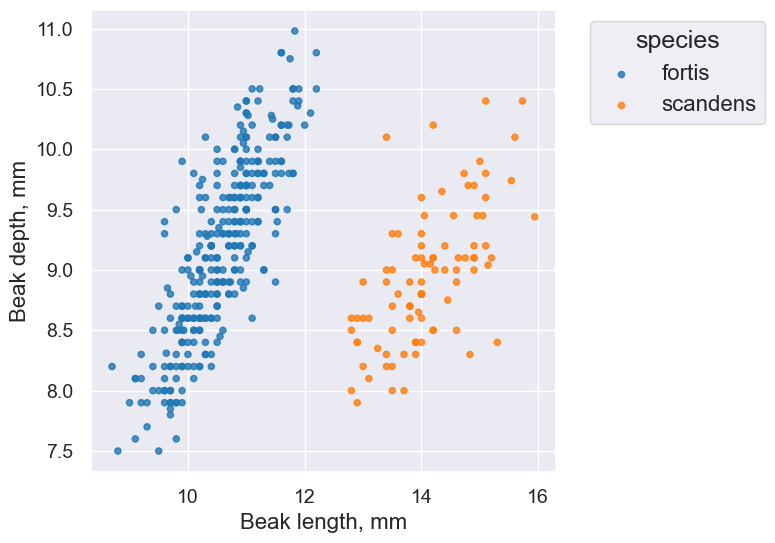
finch_1975.scatter('Beak length, mm', 'Beak depth, mm', group='species')
plot.set_title('Fortis Finches, 1975') 

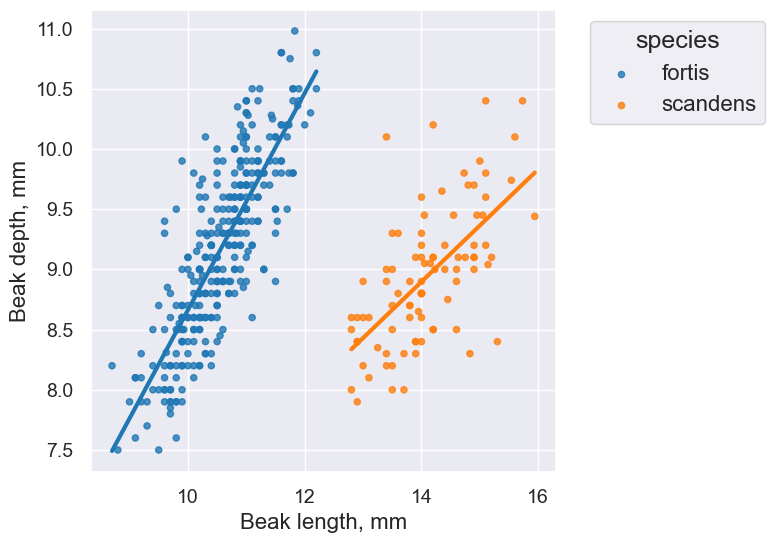
finch_1975.scatter('Beak length, mm', 'Beak depth, mm', group='species', fit_line=True)
plot.set_title('Fortis Finches, 1975') 

2. Correlation Intuition#

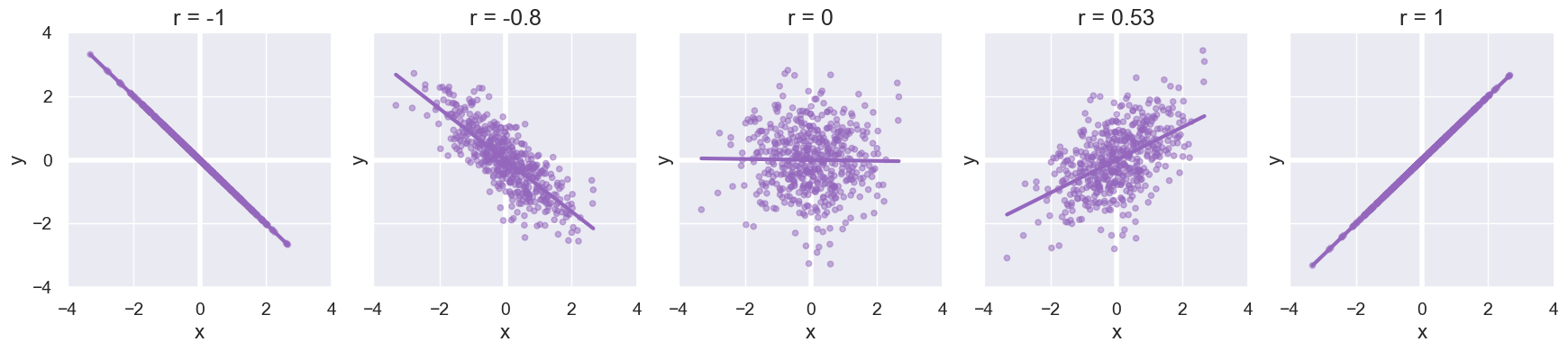
Visualize different values of r:

def make_table(r, x_mean, y_mean, size, seed=10):
    """
    Make a table of size random (x,y) points with a 
    correlation coefficient of approximately r.
    The points will be centered at (x_mean,y_mean).
    """
    rng = np.random.default_rng(seed)
    x = rng.normal(x_mean, 1, size)
    z = rng.normal(y_mean, 1, size)
    y = r*x + (np.sqrt(1-r**2))*z
    
    # Make sure the mean is *exactly* what we want :).
    table = Table().with_columns("x", x - np.mean(x) + x_mean, "y", y - np.mean(y) + y_mean)
    
    return table

def plot_table(table, color='C4', fit_line=True, **kwargs):
    """
    Plot a table of (x,y).
    """
    plot = table.scatter("x", "y",alpha=0.5, fit_line=fit_line, color=color, **kwargs)
    plot.line(x = 0, color='white', width=4, zorder=0.9)
    plot.line(y = 0, color='white', width=4, zorder=0.9)    
    plot.set_xlim(-4, 4)
    plot.set_ylim(-4, 4)
    return plot

def r_scatter(r):
    "Generate a scatter plot with a correlation approximately r"
    table = make_table(r, 0, 0, 500)
    plot = plot_table(table)
    plot.set_title('r = '+str(r))

interact(r_scatter, r = Slider(-1,1,0.01))

Here are several scatter plots with representative values of r.

Formula for r#

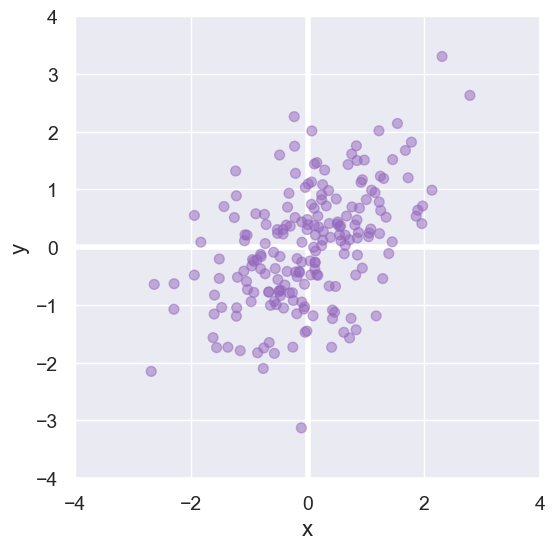
Here is a small data set we’ll use to develop a formula for computing Pearson’s correlation coefficient \(r\).

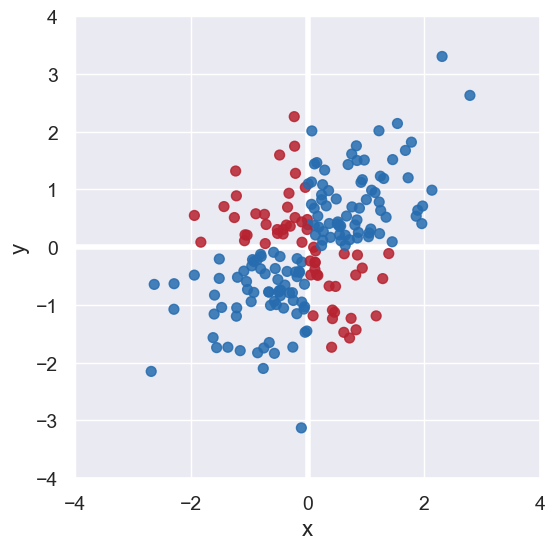
We first note that the blue points in the top-right and bottom-left quadrants reflect positive correlation between x and y. The red points in the other two quadrents reflect negative correlation.

We can determined whether a point \((x,y)\) contributes to a positive/negative association by inspecting the sign if \(x \cdot y\). Also points close to the diagonals and further away from the origin reflect much stronger correlation than those near the origin.

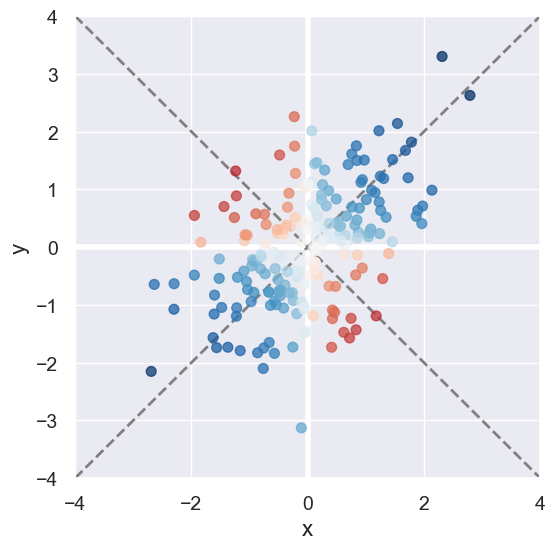
This leads us to our first way to quantify correlation: \( \sum_i x_i y_i = x_0 y_0 + x_1 y_1 + \ldots + x_n y_n \).

However, this formula can produce arbitrarily large or small numbers. For our sample data, that formula produces 93.1.

We must normalize it to be in the range -1 to 1 to ensure our coefficient is interpretable:

\[ \frac{\sum_i x_i y_i}{\sqrt{\sum_i x_i^2}\sqrt{\sum_i y_i^2}} \]

With that adjustment, our data set yields 0.48.

Now consider the data set on the left below. Unlike those above, this data is not “centered” at (0,0). That is the mean \(x\) and mean \(y\) values are not both 0. Our formula produces the correlation coefficient 0.24, but \(x\) and \(y\) are not positively correlated, but rather negatively! The issue can be seen with the plot on the right: we’ve mis-classified many points as showing positive correlation instead of negative because where they line on the plane.

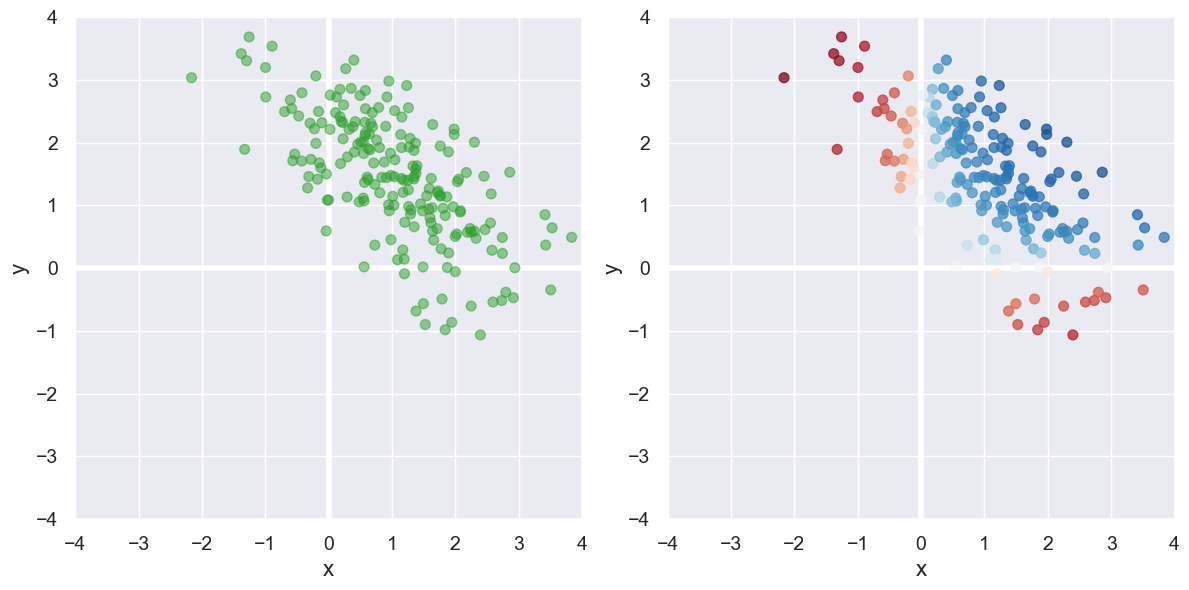
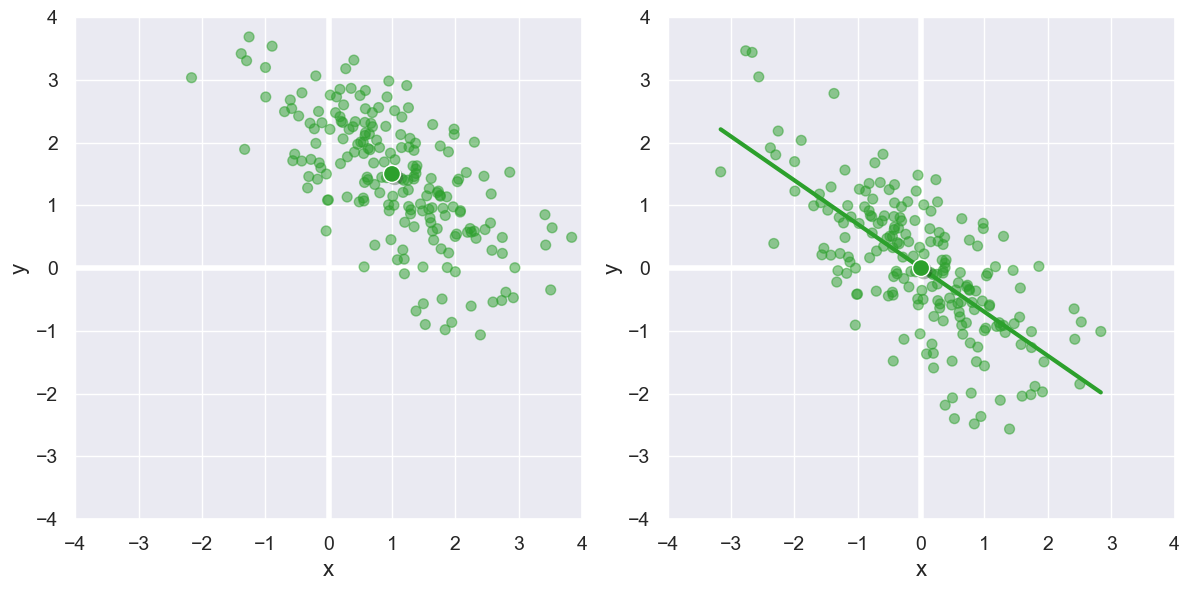
To handle this, we must recenter that data at (0,0) by subtract the mean x and mean y values \((\bar{x},\bar{y})\) from each point with our final formula for \(r\):

\[ r = \frac{ \sum_i (x_i - \bar{x})(y_i - \bar{y}) }{ \sqrt{\sum_i(x_i - \bar{x})^2}\sqrt{\sum_i(y_i - \bar{y})^2} } \]

We see that adjustment visually below, and the formula above shows \(r\) to be -0.70.

3. Implementing Pearson’s Correlation Coefficient#

Here is our formula for \(r\), given a set of points \((x_i, y_i)\):

\[ r = \frac{ \sum_i (x_i - \bar{x})(y_i - \bar{y}) }{ \sqrt{\sum_i(x_i - \bar{x})^2}\sqrt{\sum_i(y_i - \bar{y})^2} } \]

where \(\bar{x}\) is the mean of all \(x\), and \(\bar{y}\) is the mean of all \(y\).

And its implementation:

def pearson_correlation(table, x_label, y_label):
    """
    Return the correlation coefficient capturing the sign
    and strength of the association between the given columns in the
    table.
    """
    x = table.column(x_label)
    y = table.column(y_label)
    x_mean = np.mean(x)
    y_mean = np.mean(y)
    numerator = sum((x - x_mean) * (y - y_mean)) 
    denominator = np.sqrt(sum((x - x_mean)**2)) * np.sqrt(sum((y - y_mean)**2))
    return numerator / denominator 

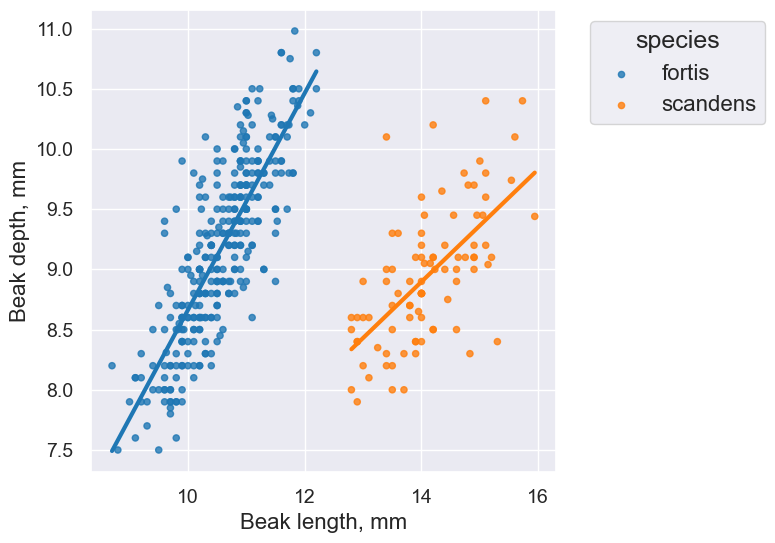
fortis_r = pearson_correlation(fortis, 'Beak length, mm', 'Beak depth, mm')
fortis_r

0.8212303385631524

scandens_r = pearson_correlation(scandens, 'Beak length, mm', 'Beak depth, mm')
scandens_r

0.624688975610796

finch_1975.scatter('Beak length, mm', 'Beak depth, mm', fit_line=True, group="species")

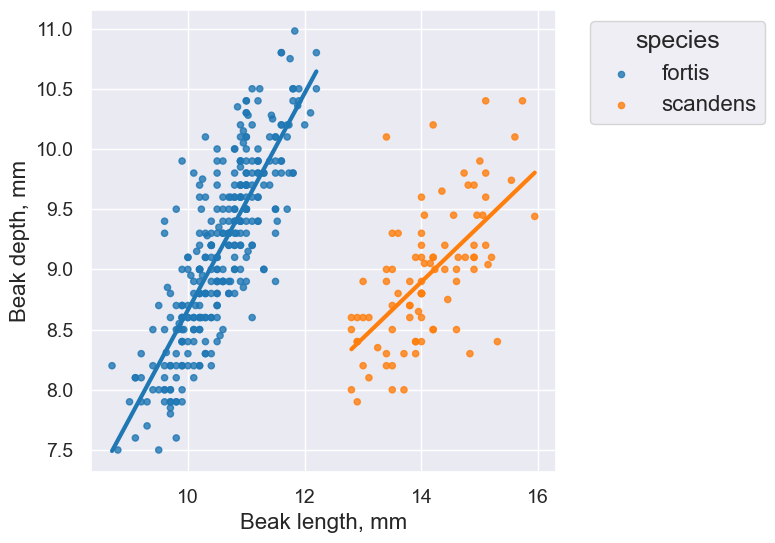
fortis_r = pearson_correlation(fortis, 'Beak length, mm', 'Beak depth, mm')
fortis_r

0.8212303385631524

scandens_r = pearson_correlation(scandens, 'Beak length, mm', 'Beak depth, mm')
scandens_r

0.624688975610796

finch_1975.scatter('Beak length, mm', 'Beak depth, mm', fit_line=True, group="species")

Switching axes shouldn’t change anything.

scandens_r = pearson_correlation(scandens, 'Beak depth, mm', 'Beak length, mm')
scandens_r

0.624688975610796

One more example#

Median sale/rental prices for homes in various cities in July 2018. Want more data? Curious how these stack up to current prices? What may be driving any changes? Checkout out Zillow, for example.

homes = Table.read_table('data/homes.csv')
homes

City	Median Sale Price	Median Rental Price
New York	429700	2372
Los Angeles	643300	2752
Chicago	219800	1636
Houston	199300	1548
Washington	397500	2132
Miami	275700	1857
Atlanta	206300	1394
Boston	456400	2365
Detroit	156100	1194
Portland	391800	1834

... (2 rows omitted)

homes.scatter('Median Sale Price', 'Median Rental Price')

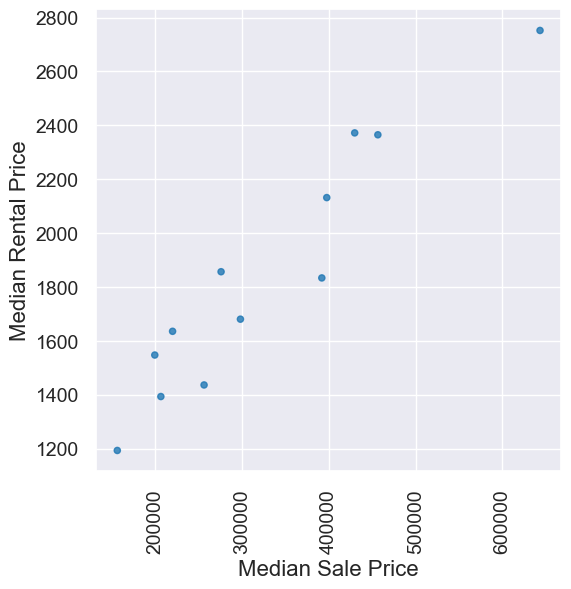
pearson_correlation(homes, 'Median Sale Price','Median Rental Price')

0.9516225800961086

4. Watch out for…#

Nonlinearity#

new_x = np.arange(-4, 4.1, 0.5)
nonlinear = Table().with_columns(
        'x', new_x,
        'y', new_x**2
    )
nonlinear.scatter('x', 'y', s=50, color='red')

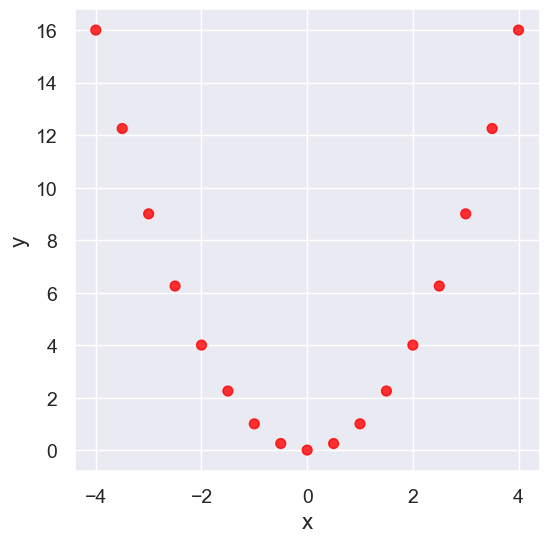
pearson_correlation(nonlinear, 'x', 'y')

0.0

Outliers#

What can cause outliers? What to do when you encounter them?

line = Table().with_columns(
        'x', make_array(1, 2, 3, 4,5),
        'y', make_array(1, 2, 3, 4,5)
    )
line.scatter('x', 'y', s=50, color='red')

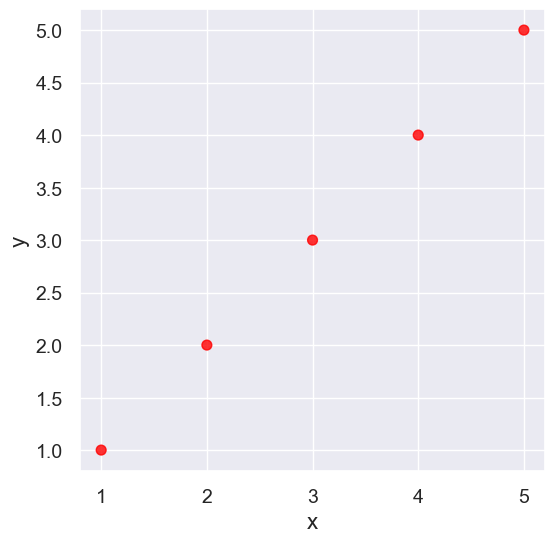
pearson_correlation(line, 'x', 'y')

0.9999999999999998

outlier = Table().with_columns(
        'x', make_array(1, 2, 3, 4, 5),
        'y', make_array(1, 2, 3, 4, 0)
    )
outlier.scatter('x', 'y', s=50, color='red')

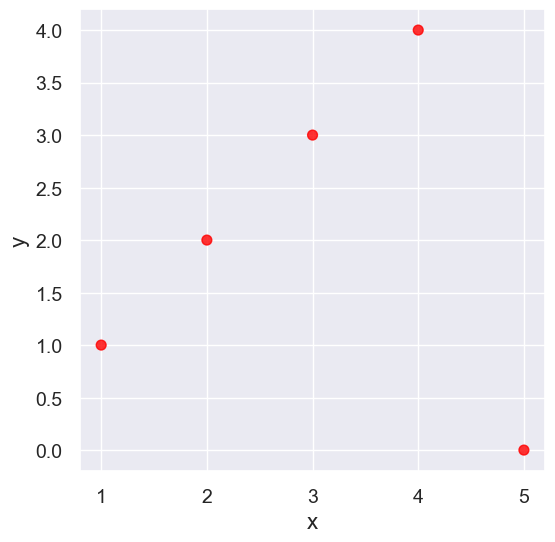
pearson_correlation(outlier, 'x', 'y')

0.0

False Correlations due to Data Aggregation#

sat2014 = Table.read_table('data/sat2014.csv').sort('State')
sat2014

State	Participation Rate	Critical Reading	Math	Writing	Combined
Alabama	6.7	547	538	532	1617
Alaska	54.2	507	503	475	1485
Arizona	36.4	522	525	500	1547
Arkansas	4.2	573	571	554	1698
California	60.3	498	510	496	1504
Colorado	14.3	582	586	567	1735
Connecticut	88.4	507	510	508	1525
Delaware	100	456	459	444	1359
District of Columbia	100	440	438	431	1309
Florida	72.2	491	485	472	1448

... (41 rows omitted)

sat2014.scatter('Critical Reading', 'Math')

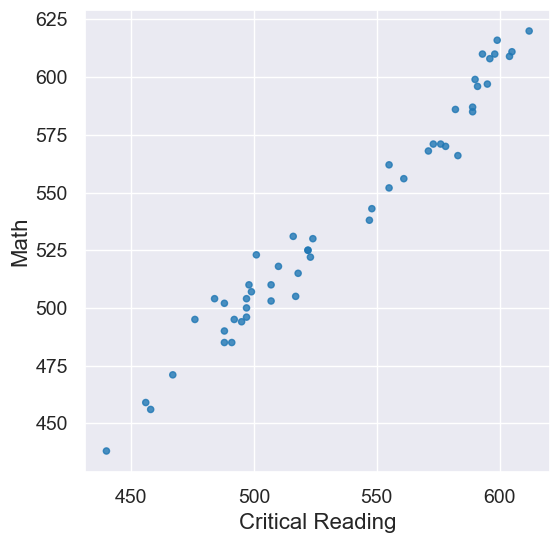
pearson_correlation(sat2014, 'Critical Reading', 'Math')

0.9847558411067432

Here is some fake data to illustrate this:

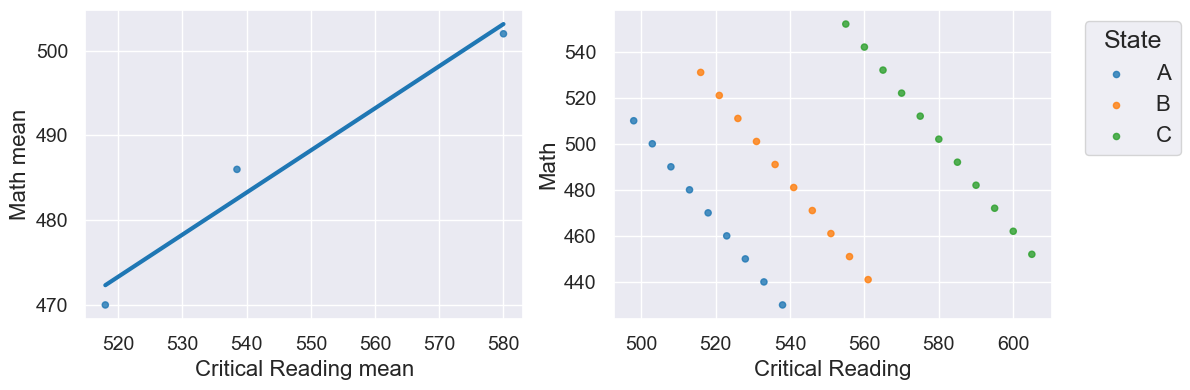
r is 0.98 on the left, but -0.09 for the un-aggregated data on the right!

CSCI 104: Data Science and Computing for All

Correlation Coefficients

Contents