Correlation

from datascience import *
from cs104 import *
import numpy as np
%matplotlib inline

Hypothesis Testing with Confidence Intervals: Biased Coin?

• Observed sample: 45 heads, 55 tails

• Null Hypothesis: Coin is not biased, so expect 50% chance of heads on each flip

• Alt Hypothesis: Coin is biased

observed_sample_size = 100
observed_num_heads = 45

observed_sample = Table().with_columns('flips', 
                                       np.append(np.full(observed_num_heads, 'heads'), 
                                                 np.full(observed_sample_size - observed_num_heads, 'tails')))
observed_sample.column('flips')

array(['heads', 'heads', 'heads', 'heads', 'heads', 'heads', 'heads',
       'heads', 'heads', 'heads', 'heads', 'heads', 'heads', 'heads',
       'heads', 'heads', 'heads', 'heads', 'heads', 'heads', 'heads',
       'heads', 'heads', 'heads', 'heads', 'heads', 'heads', 'heads',
       'heads', 'heads', 'heads', 'heads', 'heads', 'heads', 'heads',
       'heads', 'heads', 'heads', 'heads', 'heads', 'heads', 'heads',
       'heads', 'heads', 'heads', 'tails', 'tails', 'tails', 'tails',
       'tails', 'tails', 'tails', 'tails', 'tails', 'tails', 'tails',
       'tails', 'tails', 'tails', 'tails', 'tails', 'tails', 'tails',
       'tails', 'tails', 'tails', 'tails', 'tails', 'tails', 'tails',
       'tails', 'tails', 'tails', 'tails', 'tails', 'tails', 'tails',
       'tails', 'tails', 'tails', 'tails', 'tails', 'tails', 'tails',
       'tails', 'tails', 'tails', 'tails', 'tails', 'tails', 'tails',
       'tails', 'tails', 'tails', 'tails', 'tails', 'tails', 'tails',
       'tails', 'tails'], dtype='<U5')

def percent_heads(sample):
    return 100 * sum(sample == 'heads') / len(sample)

percent_heads(observed_sample.column('flips'))

45.0

# def bootstrap(observed_sample, num_trials): 

#     bootstrap_statistics = make_array()
    
#     for i in np.arange(0, num_trials): 
        
#         simulated_resample = observed_sample.sample()
#         resample_statistic = percent_heads(simulated_resample)
        
#         bootstrap_statistics = np.append(bootstrap_statistics, resample_statistic)
    
#     return bootstrap_statistics

# def percentile_method(ci_percent, bootstrap_statistics):
#     """
#     Return an array with the lower and upper bound of the ci_percent confidence interval.
#     """
#     # percent in each of the the left/right tails
#     percent_in_each_tail = (100 - ci_percent) / 2   
#     left = percentile(percent_in_each_tail, bootstrap_statistics)
#     right = percentile(100 - percent_in_each_tail, bootstrap_statistics)
#     return make_array(left, right)

bootstrap_statistics = bootstrap_statistic(observed_sample.column('flips'), percent_heads, 1000)
results = Table().with_columns("Percent Heads", bootstrap_statistics)
plot = results.hist()
left_right = confidence_interval(95, bootstrap_statistics)
plot.interval(left_right)
plot.dot(percent_heads(observed_sample.column('flips')))

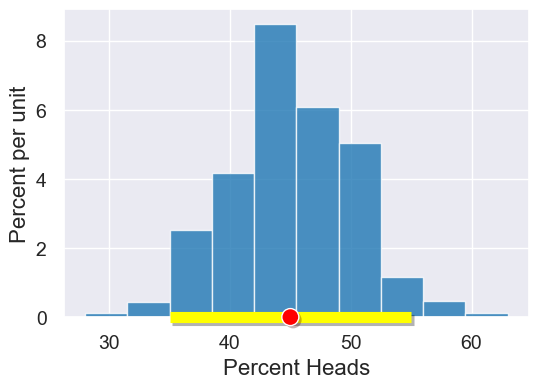
“50% heads” (Null Hypothesis) is in the 95% confidence interval, so we cannot reject the Null Hypothesis.

Finch data and visualizations

# Load finch data 
finch_1975 = Table().read_table("data/finch_beaks_1975.csv")
finch_1975.show(6)

species	Beak length, mm	Beak depth, mm
fortis	9.4	8
fortis	9.2	8.3
scandens	13.9	8.4
scandens	14	8.8
scandens	12.9	8.4
fortis	9.5	7.5

... (400 rows omitted)

fortis = finch_1975.where('species', 'fortis')
fortis.num_rows

316

scandens = finch_1975.where('species', 'scandens')
scandens.num_rows

90

fortis.scatter('Beak length, mm', 'Beak depth, mm')
plots.title('Fortis Finches, 1975');

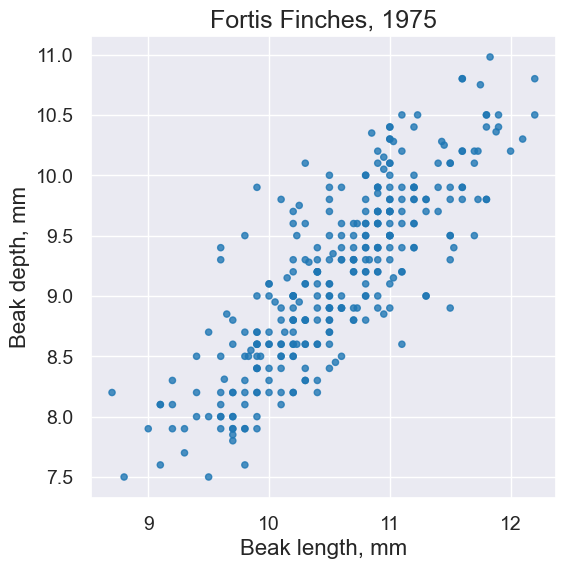
fortis.scatter('Beak length, mm', 'Beak depth, mm', fit_line=True)
plots.title('Fortis Finches, 1975'); 

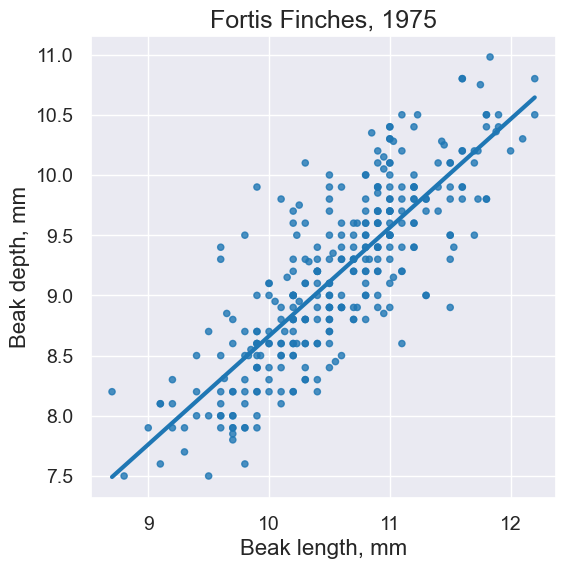
finch_1975.scatter('Beak length, mm', 'Beak depth, mm', group='species')

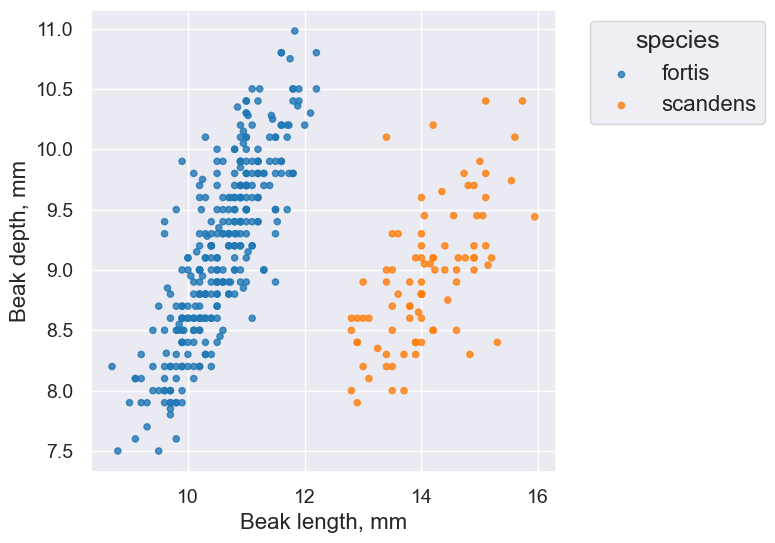
Correlation

Visualize different values of r:

def r_scatter(r):
    "Generate a scatter plot with a correlation approximately r"
    x = np.random.normal(0, 1, 500)
    z = np.random.normal(0, 1, 500)
    y = r*x + (np.sqrt(1-r**2))*z
    table = Table().with_columns("x", x, "y", y)
    plot = table.scatter("x", "y",alpha=0.5)
    plot.set_xlim(-4, 4)
    plot.set_ylim(-4, 4)
    plot.set_title('r = '+str(r))

The following cell contains an interactive visualization. You won’t see the visualization on this web page, but you can view and interact with it if you run this notebook on our server here.

interact(r_scatter, r = Slider(-1,1,0.01))

Computing Pearson’s Correlation Coefficient

The formula: \( r = \frac{\sum(x - \bar{x})(y - \bar{y})}{\sqrt{\sum(x - \bar{x})^2} \sqrt{\sum(y - \bar{y})^2}} \)

#Katie: I'd vote making this an API call 

def pearson_correlation(table, x_label, y_label):
    x = table.column(x_label)
    y = table.column(y_label)
    x_mean = np.mean(x)
    y_mean = np.mean(y)
    numerator = sum((x - x_mean) * (y - y_mean)) 
    denominator = np.sqrt(sum((x - x_mean)**2)) * np.sqrt(sum((y - y_mean)**2))
    return numerator / denominator 

fortis_r = pearson_correlation(fortis, 'Beak length, mm', 'Beak depth, mm')
fortis_r

0.8212303385631524

scandens_r = pearson_correlation(scandens, 'Beak length, mm', 'Beak depth, mm')
scandens_r

0.624688975610796

finch_1975.scatter('Beak length, mm', 'Beak depth, mm', fit_line=True, group="species")

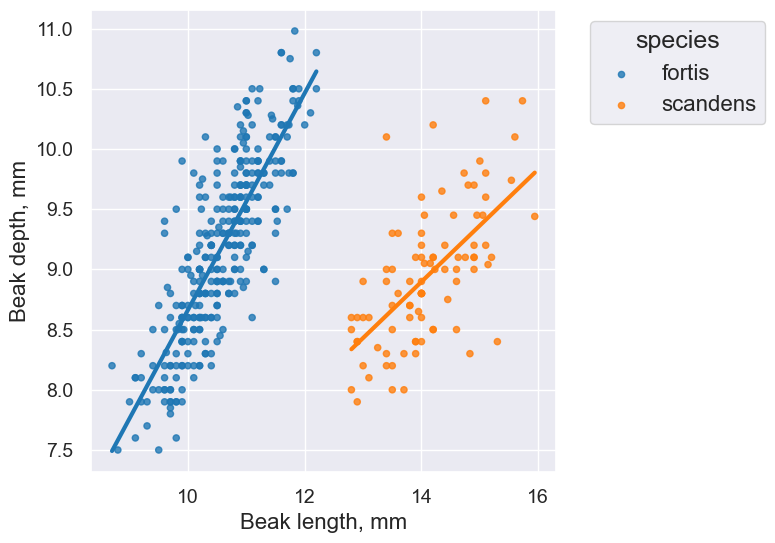
CIs for Correlation coefficient via bootstrapping

def bootstrap_finches(observed_sample, num_trials): 

    bootstrap_statistics = make_array()
    
    for i in np.arange(0, num_trials): 
        
        simulated_resample = observed_sample.sample()
        
        # this changes for this example
        resample_statistic = pearson_correlation(simulated_resample, 'Beak length, mm', 'Beak depth, mm')
        
        bootstrap_statistics = np.append(bootstrap_statistics, resample_statistic)
    
    return bootstrap_statistics

fortis_bootstraps = bootstrap_finches(fortis, 10000)

scandens_bootstraps = bootstrap_finches(scandens, 10000)

fortis_ci = percentile_method(95, fortis_bootstraps)
print('Fortis r = ', fortis_r)
print('Fortis CI=', fortis_ci)

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
Cell In[25], line 1
----> 1 fortis_ci = percentile_method(95, fortis_bootstraps)
      2 print('Fortis r = ', fortis_r)
      3 print('Fortis CI=', fortis_ci)

NameError: name 'percentile_method' is not defined

scandens_ci = percentile_method(95, scandens_bootstraps)
print('Scandens r = ', scandens_r)
print('Scandens CI=', scandens_ci)

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
Cell In[26], line 1
----> 1 scandens_ci = percentile_method(95, scandens_bootstraps)
      2 print('Scandens r = ', scandens_r)
      3 print('Scandens CI=', scandens_ci)

NameError: name 'percentile_method' is not defined

Table().with_columns('fortis', fortis_bootstraps, 'scandens', scandens_bootstraps).hist(bins=40)

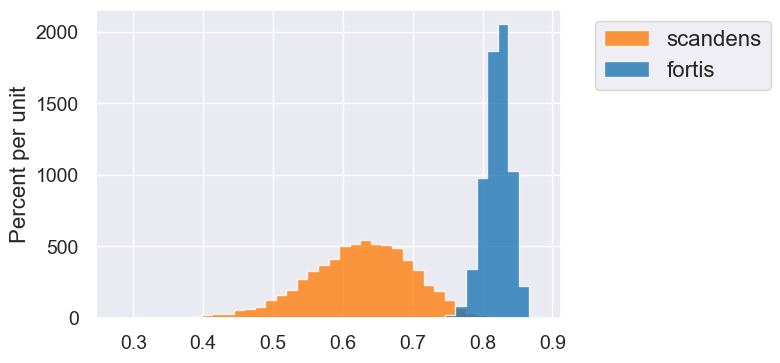
Switching Axes

fortis.scatter('Beak length, mm', 'Beak depth, mm')

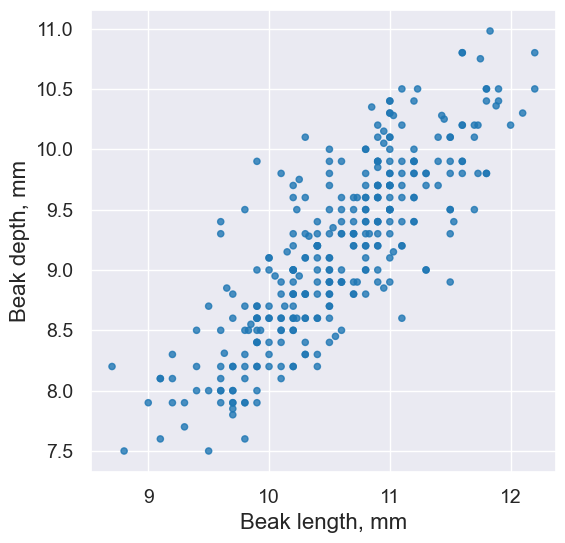
pearson_correlation(fortis, 'Beak length, mm', 'Beak depth, mm')

0.8212303385631524

fortis.scatter('Beak depth, mm','Beak length, mm')

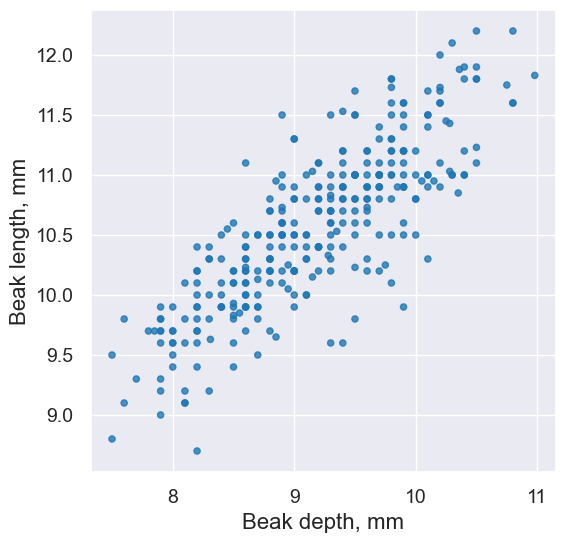
pearson_correlation(fortis, 'Beak depth, mm', 'Beak length, mm')

0.8212303385631524

Watch out for…

Nonlinearity

new_x = np.arange(-4, 4.1, 0.5)
nonlinear = Table().with_columns(
        'x', new_x,
        'y', new_x**2
    )
nonlinear.scatter('x', 'y', s=50, color='red')

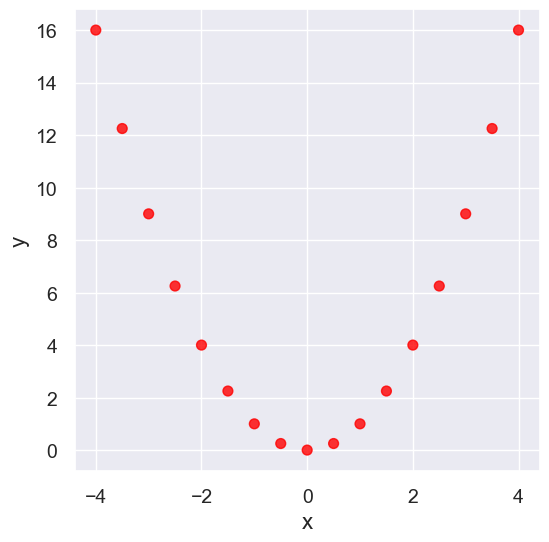
pearson_correlation(nonlinear, 'x', 'y')

0.0

Outliers

What can cause outliers? What to do when you encounter them?

line = Table().with_columns(
        'x', make_array(1, 2, 3, 4,5),
        'y', make_array(1, 2, 3, 4,5)
    )
line.scatter('x', 'y', s=50, color='red')

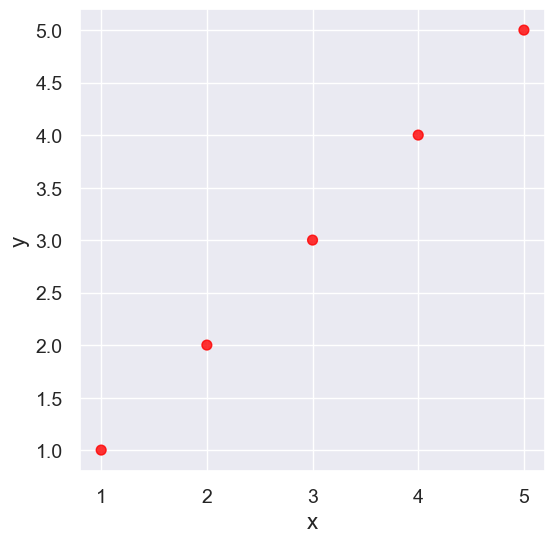
pearson_correlation(line, 'x', 'y')

0.9999999999999998

outlier = Table().with_columns(
        'x', make_array(1, 2, 3, 4, 5),
        'y', make_array(1, 2, 3, 4, 0)
    )
outlier.scatter('x', 'y', s=50, color='red')

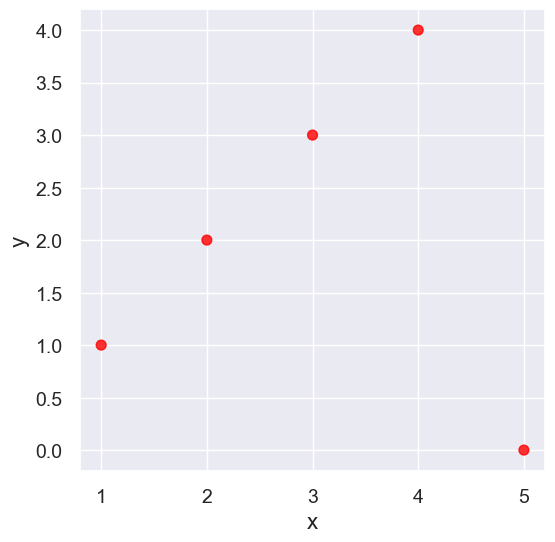
pearson_correlation(outlier, 'x', 'y')

0.0

False Correlations due to Data Aggregation

sat2014 = Table.read_table('data/sat2014.csv').sort('State')
sat2014

State	Participation Rate	Critical Reading	Math	Writing	Combined
Alabama	6.7	547	538	532	1617
Alaska	54.2	507	503	475	1485
Arizona	36.4	522	525	500	1547
Arkansas	4.2	573	571	554	1698
California	60.3	498	510	496	1504
Colorado	14.3	582	586	567	1735
Connecticut	88.4	507	510	508	1525
Delaware	100	456	459	444	1359
District of Columbia	100	440	438	431	1309
Florida	72.2	491	485	472	1448

... (41 rows omitted)

sat2014.scatter('Critical Reading', 'Math')

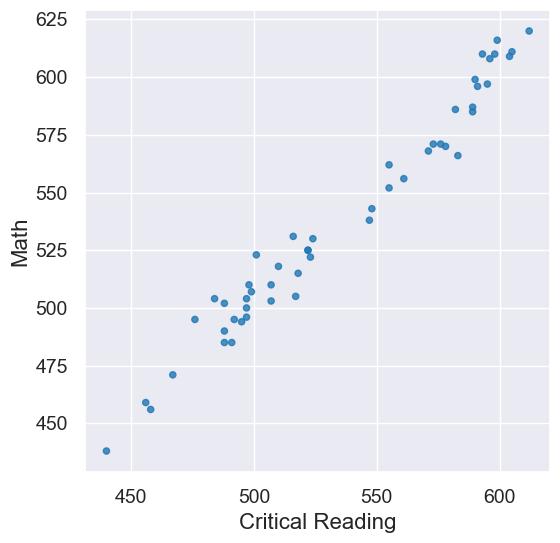
pearson_correlation(sat2014, 'Critical Reading', 'Math')

0.9847558411067432