Randomized Controlled Experiments#

from datascience import *
from cs104 import *
import numpy as np
%matplotlib inline

1. Warm-up Permutation Test#

survey = Table().read_table('data/prelab01-survey-fall2025.csv')
survey = survey.relabeled('Left or right handed? ', 'Left or Right Handed')  # clean up label
survey = survey.where('Left or Right Handed', are.not_equal_to('Ambidextrous'))
survey
Favorite icecream flavor Favorite planet Height (in inches) Distance Home (in miles) Birthday month Left or Right Handed
Mint chocolate chip Neptune 67 49 September Right handed
Vanilla Neptune 72 178 December Right handed
Purple Cow Earth 72 3058.6 April Right handed
Strawberry Earth 62 66 July Right handed
Strawberry Earth 66.5 185 June Left handed
Mint chocolate chip Saturn 65 2851.8 January Right handed
Purple Cow Mars 64 162 February Right handed
Mint chocolate chip Earth 68.5 120 April Right handed
Mint chocolate chip Earth 66 18.4 January Right handed
Chocolate Earth 68 146 January Right handed

... (48 rows omitted)

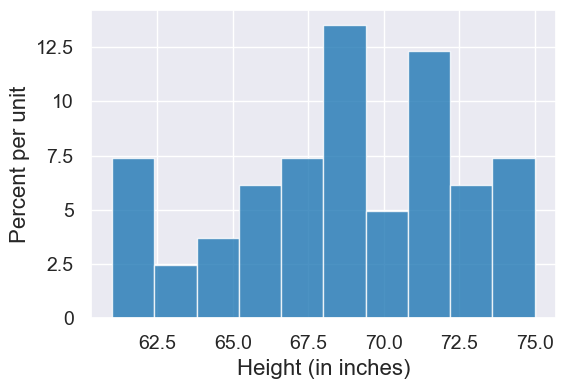
survey.hist('Height (in inches)')
../_images/23-randomized-controlled-experiments_5_0.png 
survey.group('Left or Right Handed')
Left or Right Handed count
Left handed 8
Right handed 50 
observed = abs_difference_of_means(survey, 'Left or Right Handed', 'Height (in inches)')
observed

0.20049999999999102

Is the height difference significant?

results = simulate_permutation_statistic(survey, 'Left or Right Handed', 'Height (in inches)', 5000)

plot = Table().with_columns('abs_difference_of_means', results).hist(left_end=observed)
plot.set_title('Null hypothesis empirical distibution')
plot.dot(observed)
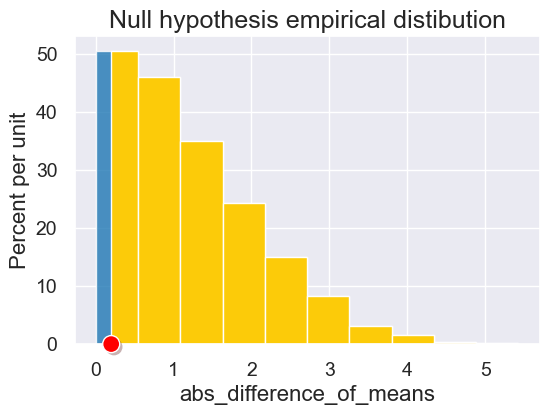
../_images/23-randomized-controlled-experiments_10_0.png 
p_value = empirical_pvalue(results, observed)
p_value

0.9064

2. Randomized Controlled Experiment with BTA#

rct = Table.read_table('data/bta.csv')
rct.sample(10)
Group Result
Treatment 1
Treatment 0
Control 1
Control 0
Treatment 0
Control 0
Control 0
Control 0
Control 1
Control 0 
rct.group('Group')
Group count
Control 16
Treatment 15 
rct.pivot('Result', 'Group')
Group 0.0 1.0
Control 14 2
Treatment 6 9 
rct.group('Group', np.mean)
Group Result mean
Control 0.125
Treatment 0.6

Permutation Testing#

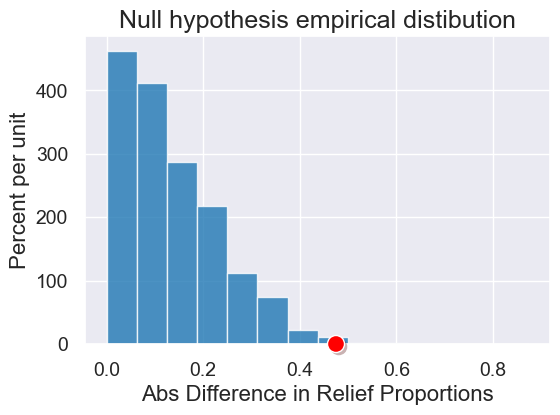
observed_statistic = abs_difference_of_means(rct, 'Group', 'Result')
observed_statistic

0.475

type(observed_statistic)

float

results = simulate_permutation_statistic(rct, 'Group', 'Result', 2000)

plot = Table().with_columns('Abs Difference in Relief Proportions', results).hist(bins=np.arange(0,0.9,1/16))
plot.set_title('Null hypothesis empirical distibution')
plot.dot(observed_statistic)
../_images/23-randomized-controlled-experiments_21_0.png 
p_value = empirical_pvalue(results, observed_statistic)
p_value

0.008

3. Sample Size, Effect Size, and P-values#

What’s the relationship between effect size, sample size, and p-value?

What we had before.

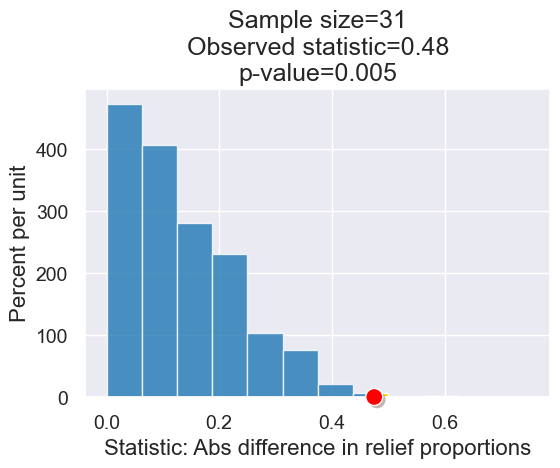
../_images/23-randomized-controlled-experiments_27_0.png

What if the effect size was slightly smaller? What if the sample size was bigger?

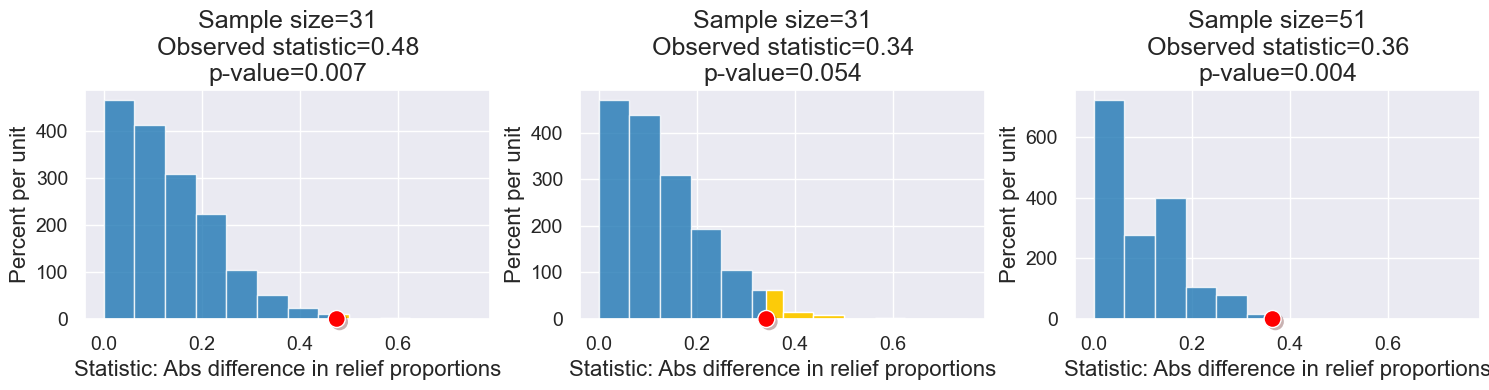
../_images/23-randomized-controlled-experiments_29_0.png

Let’s look at all these relationships at once!

interact(back_pain_exploration, 
         observed_sample_size=Slider(10, 128, 1), 
         treatment_prop_effective=Slider(0.05, 0.95, 0.01),
         control_prop_effective=Slider(0.05, 0.95, 0.01))

Here’s an animation showing the effects above.