Probability

from datascience import *
from cs104 import *
import numpy as np
%matplotlib inline

1. Random Choice, Loops, Simulation Review

In the last lecture, we wrote the following code to simulate tossing a coin 100 times and counting the number of heads.

coin = make_array('heads', 'tails')

np.random.choice(coin)

'heads'

flips = np.random.choice(coin, 100)
flips

array(['heads', 'heads', 'tails', 'tails', 'tails', 'tails', 'tails',
       'heads', 'tails', 'tails', 'heads', 'tails', 'tails', 'tails',
       'tails', 'tails', 'tails', 'heads', 'heads', 'heads', 'heads',
       'heads', 'heads', 'heads', 'tails', 'tails', 'heads', 'tails',
       'heads', 'heads', 'tails', 'heads', 'tails', 'tails', 'heads',
       'tails', 'tails', 'tails', 'tails', 'tails', 'heads', 'heads',
       'tails', 'heads', 'tails', 'tails', 'tails', 'tails', 'tails',
       'heads', 'tails', 'tails', 'heads', 'tails', 'heads', 'heads',
       'heads', 'tails', 'tails', 'tails', 'heads', 'tails', 'tails',
       'tails', 'tails', 'tails', 'heads', 'heads', 'heads', 'heads',
       'tails', 'heads', 'tails', 'heads', 'heads', 'heads', 'heads',
       'tails', 'heads', 'tails', 'heads', 'tails', 'tails', 'heads',
       'tails', 'heads', 'tails', 'heads', 'tails', 'tails', 'tails',
       'heads', 'heads', 'tails', 'tails', 'heads', 'tails', 'heads',
       'tails', 'heads'], dtype='<U5')

np.count_nonzero(flips == 'heads')

44

def heads_in_100_flips():
    """ Returns the number of heads in 100 flips of
    a fair coin """
    coin = make_array('heads', 'tails')
    flips = np.random.choice(coin, 100)
    return np.count_nonzero(flips == 'heads')

heads_in_100_flips()

46

We also wrote a simulation look using our algorithm to emperically estimate the probability of getting between 40 and 60 heads in 100 flips.

Generic simulation algorithm:

• Repeat N times:

  • Simulate one trial

  • Record the outcome

• Analyze outcomes for all trials

We record the outcomes by appending them to an array.

# Create an empty array
outcomes = make_array()

# Run this a bunch -- each run adds one more element to outcomes
num_heads = heads_in_100_flips()
outcomes = np.append(outcomes, num_heads)
outcomes

array([50.])

Now make a loop!

num_trials = 10000
outcomes = make_array()
for i in np.arange(0, num_trials):
    num_heads = heads_in_100_flips()
    outcomes = np.append(outcomes, num_heads)
    
outcomes

array([53., 55., 55., ..., 41., 47., 52.])

simulated_results = Table().with_columns('Heads in 100 flips', 
                                        outcomes)
plot = simulated_results.hist(bins=np.arange(30, 70, 1))
plot.interval(40,60)

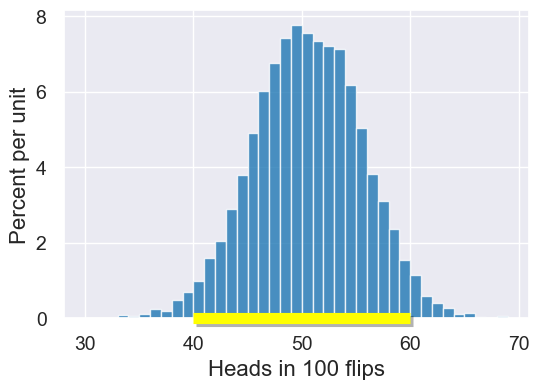
target_range = simulated_results.where("Heads in 100 flips", 
                                       are.between(40,60))
proportion_40_to_60 = target_range.num_rows / simulated_results.num_rows
print('proportion between 40 and 60:', proportion_40_to_60)

proportion between 40 and 60: 0.9539

2. A general simulation function

Let’s make a reusable version of our simulation. That is, let’s make a function to do the work and produce the outcomes array. We can start with our simulation loop above:

num_trials = 10000
outcomes = make_array()
for i in np.arange(0, num_trials):
    num_heads = heads_in_100_flips()
    outcomes = np.append(outcomes, num_heads)
outcomes

array([51., 54., 46., ..., 47., 54., 59.])

This code depends on two pieces of information specific to the simulation we wish to perform:

1. the number of trials (num_trials)

2. the code to compute the outcome of one trial (eg: heads_in_100_flips(). That code would need to change if we simulated the number of tails in 200 flips, the sum of 20 dice rolls, or any other kind outcome.

To enable us to use our general function with different numbers of trials or different functions to make the outcomes, we write the function with those two items as parameters:

def simulate(make_one_outcome, num_trials):
    """
    Return an array of num_trials values, each 
    of which was created by calling make_one_outcome().
    """
    outcomes = make_array()
    for i in np.arange(0, num_trials):
        outcome = make_one_outcome()
        outcomes = np.append(outcomes, outcome)

    return outcomes

We can then call simulate as follows:

simulate(heads_in_100_flips, 10)

array([55., 50., 51., 57., 53., 51., 54., 54., 49., 55.])

Or if we are interested in the sum of 20 dice rolls, we call it as follows:

def sum_twenty_dice():
    dice = np.arange(1,7)
    roll_20_dice = np.random.choice(dice, 20)
    return sum(roll_20_dice)

simulate(sum_twenty_dice, 5)

array([50., 71., 66., 75., 56.])

Notice how we can design new simulations without starting from scratch! We write a function to compute one outcome, and then reuse simulate with the number of trials we wish to perform.

And just for fun…

twenty_dice = simulate(sum_twenty_dice, 100000)
Table().with_columns('Sum of 20 dice', twenty_dice).hist(bins=np.arange(40,100,1))

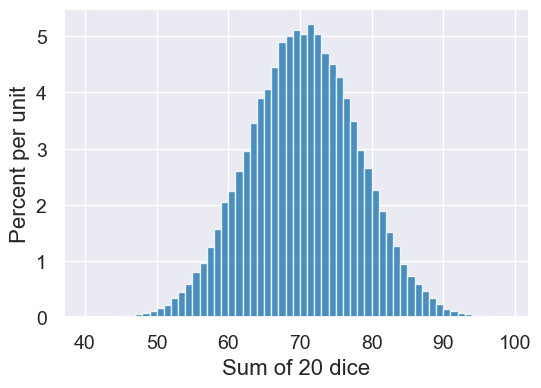
Does this look like any other histogram we saw today?

3. The Monty Hall Problem

• Three doors hide two goats and a car.

• You pick one of three doors.

• A different door is opened to reveal a goat.

• You must decide which door has the car. You can stick with your original choice, or you can switch to the other unopened door.

Which strategy wins the car with higher probability?

First, we’ll define functions that give us the result of one trial. Both pick the initial door at random, and then determine which door the player ultimately selects based on our two strategies.

prizes = make_array('goat', 'goat', 'car')

def monty_hall_game_staying_strategy():
    """
    Return what player wins if they stick with their original choice
    """
    return np.random.choice(prizes)

def monty_hall_game_switching_strategy():
    """
    Return what player wins if they switch with their original choice
    """
    contestant_guess = np.random.choice(prizes)
    if contestant_guess == 'car':
        # Revealed door is one goat ...
        # ... and the remaining door is the second goat.
        return 'goat'
    else:
        # Releaved door is the second goat ...
        # ... and the remaining door is the car.
        return 'car'

monty_hall_game_staying_strategy()

'goat'

monty_hall_game_switching_strategy()

'goat'

Ooo! We get to use our simulate function!

outcomes_staying = simulate(monty_hall_game_staying_strategy, 10)
outcomes_staying

array(['car', 'car', 'goat', 'goat', 'car', 'goat', 'goat', 'car', 'goat',
       'car'], dtype='<U32')

num_trials = 10000
outcomes_staying = simulate(monty_hall_game_staying_strategy, num_trials)
stay_and_win = np.count_nonzero(outcomes_staying == "car") / len(outcomes_staying)
print("Probability of winning a car if we always stay:", stay_and_win)

Probability of winning a car if we always stay: 0.3274

outcomes_switching =  simulate(monty_hall_game_switching_strategy, num_trials)
switch_and_win = np.count_nonzero(outcomes_switching == "car")/len(outcomes_switching)
print("Probability of winning a car if we always switch", switch_and_win)

Probability of winning a car if we always switch 0.6697

Would we trust the probabilities approximated by our simulation more or less if we increase the number of trials?