Loops

from datascience import *
from cs104 import *
import numpy as np
%matplotlib inline

1. Think-Pair-Share: Leap Years

A year is a leap year if:

• The year is divisible by 4 but not divisible by 100, or

• The year is divisible by 400.

Complete the following function that returns True only when year is a leap year:

def is_leap_year(year):
    ...

Note: We can test if year is divisible by 4 using the % (modulo) operator: year % 4 == 0.

Here’s one solution:

# This version uses if statements to distinguish the three cases.
def is_leap_year(year):
    if year % 4 == 0 and year % 100 != 0:
        return True
    elif year % 400 == 0:
        return True
    else:
        return False

Here’s another that uses a different approach:

# This version embraces Boolean comparisions and operators to achieve 
# the same effect.
def is_leap_year(year):
    return ((year % 4 == 0) and (year % 100) != 0) or year % 400 == 0

is_leap_year(2024)

True

is_leap_year(2023)

False

# more thorough checks
check(is_leap_year(2024))
check(is_leap_year(2000))
check(not is_leap_year(2023))
check(not is_leap_year(2200))

2. Simulation

Think-pair-share with Dice

Suppose your friend proposes that you switch your electronic version of Monopoly so players roll one dice and multiply its value by two instead rather than the more standard way of rolling two dice and summing their values.

Which scenario will give you a higher score on average?

• Option A. Roll 2 dice and sum their values.

• Option B. Roll one dice and multiply it’s value by two.

Random Selection

dice = np.arange(1,7)
dice

array([1, 2, 3, 4, 5, 6])

Here, np.random.choice randomly picks one item from the array and it is equally likely to pick any of the items.

np.random.choice(dice)

4

We can repeat the process by calling a second argument.

np.random.choice(dice, 10)

array([3, 5, 3, 4, 4, 3, 1, 2, 3, 1])

Of 100 rolls, how many of them equal 6?

rolls = np.random.choice(dice,100)
np.count_nonzero(rolls == 6)

15

What’s the mean of all the rolls?

np.mean(rolls)

3.35

Simulating the Question

N = 1000000 #Roll the dice 1 million times 
option_a = np.random.choice(dice, N) + np.random.choice(dice, N)
option_b = 2 * np.random.choice(dice, N)

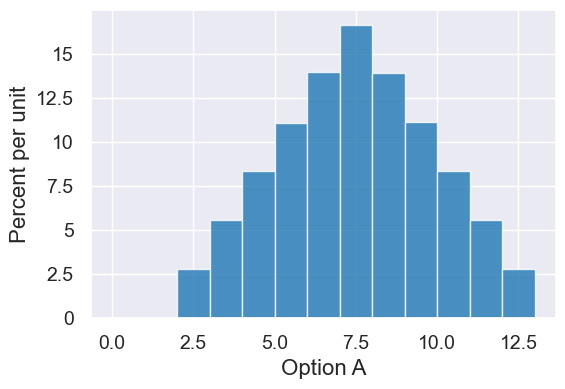
print("Option A Mean: ", np.mean(option_a))
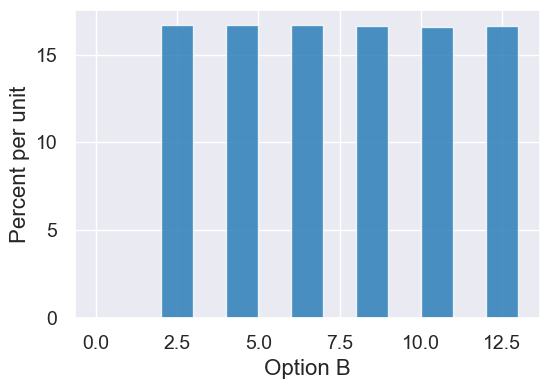
print("Option B Mean: ", np.mean(option_b))

Option A Mean:  6.99894
Option B Mean:  6.993196

samples = Table().with_columns("Option A", option_a, "Option B", option_b)
samples.hist("Option A", bins=np.arange(0,14))
samples.hist("Option B", bins=np.arange(0,14))

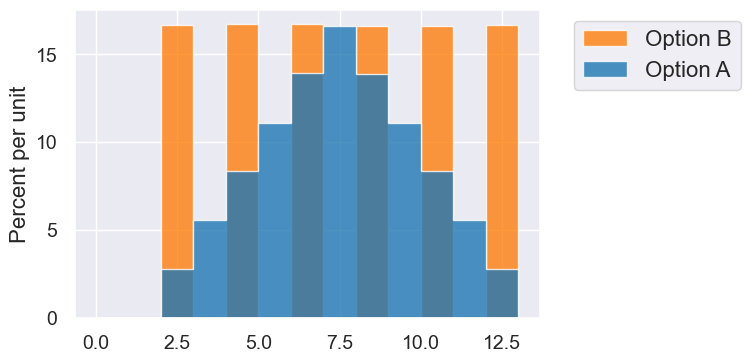
samples.hist(bins=np.arange(0,14))

3. Loops

How can we compute the average roll in option_a without using np.mean?

sum(option_a) / len(option_a)

6.99894

What if we can’t use sum?

We need to be able to do the same thing to every element in the array, namely add it to a tally we’re keeping. Loops let us do the same thing repeatedly.

np.arange(0, 5)

array([0, 1, 2, 3, 4])

for i in np.arange(0,5):
    print("iteration", i)

iteration 0
iteration 1
iteration 2
iteration 3
iteration 4

Within the for loop, we often update variables and accumulate values.

option_a

array([ 4,  7,  7, ...,  8,  8, 11])

total = 0
for i in option_a:
    total = total + i

print('total =',total, '   average =', total / len(option_a))

total = 6998940    average = 6.99894

Let’s generalize this function! We’ve been using sum all along but now we have the tools to build sum ourselves.

def sum(numbers):
    total = 0
    for i in numbers:
        total = total + i
    return total

sum(option_a)

6998940

How do we change sum to only sum up the odd numbers in numbers?

def sum_odd(numbers):
    total = 0
    for i in numbers:
        if i % 2 == 1:
            total = total + i
    return total

sum_odd(option_a)

3494852

Ooo! An if inside a for loop!

You can iterate over other types of arrays too:

for fruit in make_array("Bananas", 
                        "Apples", 
                        "Oranges"): 
    print(fruit)

Bananas
Apples
Oranges

for value in np.arange(0,3):
    print(value)

0
1
2

trees = Table().read_table('data/hopkins-trees.csv').take(0,1,2)

for tree in trees.column('common name'):
    print(tree)

Maple, striped
Maple, red
Maple, sugar

4. Simulation using loops

Think-Pair-Share

If you flip a coin 100 times, what are the odds you get between 40 and 60 heads?

Simulating One Trial

coin = make_array('heads', 'tails')

np.random.choice(coin)

'heads'

flips = np.random.choice(coin, 100)
flips

array(['heads', 'tails', 'tails', 'tails', 'heads', 'tails', 'heads',
       'tails', 'heads', 'heads', 'heads', 'tails', 'heads', 'tails',
       'tails', 'heads', 'heads', 'tails', 'heads', 'tails', 'heads',
       'tails', 'tails', 'tails', 'heads', 'tails', 'heads', 'tails',
       'heads', 'tails', 'heads', 'heads', 'heads', 'heads', 'heads',
       'heads', 'tails', 'heads', 'heads', 'tails', 'tails', 'tails',
       'heads', 'heads', 'tails', 'heads', 'tails', 'heads', 'heads',
       'tails', 'tails', 'heads', 'heads', 'heads', 'tails', 'tails',
       'heads', 'tails', 'heads', 'tails', 'heads', 'tails', 'heads',
       'tails', 'tails', 'heads', 'heads', 'heads', 'heads', 'tails',
       'heads', 'heads', 'tails', 'heads', 'tails', 'heads', 'tails',
       'heads', 'heads', 'heads', 'tails', 'tails', 'tails', 'heads',
       'heads', 'tails', 'tails', 'tails', 'tails', 'tails', 'heads',
       'heads', 'tails', 'tails', 'heads', 'tails', 'tails', 'tails',
       'heads', 'tails'], dtype='<U5')

np.count_nonzero(flips == 'heads')

51

The same code inside a function:

def heads_in_100_flips():
    """ Returns the number of heads in 100 flips of
    a fair coin """
    coin = make_array('heads', 'tails')
    flips = np.random.choice(coin, 100)
    return np.count_nonzero(flips == 'heads')

Run it a bunch!

heads_in_100_flips()

46

Appending to an array of outcomes

outcomes = make_array()

One simulation: run it a bunch!

num_heads = heads_in_100_flips()
outcomes = np.append(outcomes, num_heads)
outcomes

array([53.])

Let’s use a for loop to repeat 1000 times the outcome we care about–counting the number of heads in 100 flips.

outcomes = make_array()
num_trials = 10000
for i in np.arange(0, num_trials):
    num_heads = heads_in_100_flips()
    outcomes = np.append(outcomes, num_heads)
    
outcomes

array([51., 44., 46., ..., 55., 50., 65.])

simulated_results = Table().with_column('Heads in 100 flips', 
                                        outcomes)

plot = simulated_results.hist(bins=np.arange(30, 70, 1))
plot.interval(40,60)

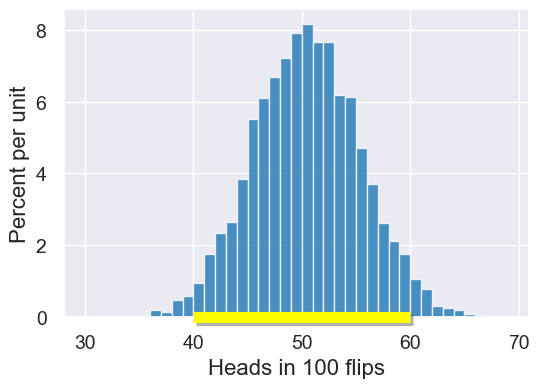
target_range = simulated_results.where("Heads in 100 flips", 
                                       are.between(40,60))

target_range.num_rows / simulated_results.num_rows

0.9566

5. A general simulation function

Let’s make a reusable version of our simulation. That is, let’s make a function to do the work and produce the outcomes array. We can start with our simulation loop above:

outcomes = make_array()
num_trials = 10000
for i in np.arange(0, num_trials):
    num_heads = heads_in_100_flips()
    outcomes = np.append(outcomes, num_heads)
outcomes

array([50., 47., 51., ..., 44., 50., 49.])

This code depends on two pieces of information specific to the simulation we wish to perform:

1. the number of trials (num_trials)

2. the code to compute the outcome of one trial (eg: heads_in_100_flips(). That code would need to change if we simulated the number of tails in 200 flips, the sum of 20 dice rolls, or any other kind outcome.

To enable us to use our general function with different numbers of trials or different functions to make the outcomes, we write the function with those two items as parameters:

def simulate(make_one_outcome, num_trials):
    """
    Return an array of num_trials values, each 
    of which was created by calling make_one_outcome().
    """
    outcomes = make_array()
    for i in np.arange(0, num_trials):
        outcome = make_one_outcome()
        outcomes = np.append(outcomes, outcome)

    return outcomes

We can then call simulate as follows:

simulate(heads_in_100_flips, 10)

array([55., 52., 44., 53., 57., 49., 47., 58., 44., 60.])

Or if we are interested in the sum of 20 dice rolls, we call it as follows:

dice = np.arange(1,7)
dice

array([1, 2, 3, 4, 5, 6])

def sum_twenty_dice():
    roll_20_dice = np.random.choice(dice, 20)
    return sum(roll_20_dice)

simulate(sum_twenty_dice, 5)

array([78., 67., 75., 60., 58.])

Notice how we can design new simulations without starting from scratch! We write a function to compute one outcome, and then reuse simulate with the number of trials we wish to perform.

And just for fun…

twenty_dice = simulate(sum_twenty_dice, 100000)
Table().with_columns('Sum of 20 dice', twenty_dice).hist(bins=np.arange(40,100,1))

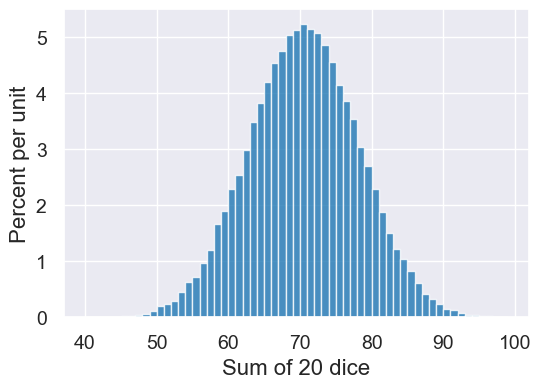
Does this look like any other histogram we saw today?