Groups#

from datascience import *
from cs104 import *
import numpy as np
%matplotlib inline

1. Functions#

Apply#

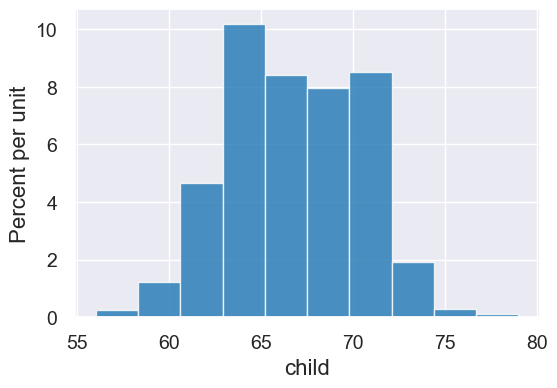
heights_original = Table().read_table('data/galton.csv')
heights = heights_original.select('father', 'mother', 'childHeight')
heights = heights.relabeled('childHeight', 'child')
heights.show(5)

father	mother	child
78.5	67	73.2
78.5	67	69.2
78.5	67	69
78.5	67	69
75.5	66.5	73.5

... (929 rows omitted)

heights.hist('child')

There are times we want to perform mathematical operations columns of the table but can’t use array broadcasting…

min(heights.column('child'), 72)  # will cause an error

---------------------------------------------------------------------------
ValueError                                Traceback (most recent call last)
Cell In[6], line 1
----> 1 min(heights.column('child'), 72)  # will cause an error

ValueError: The truth value of an array with more than one element is ambiguous. Use a.any() or a.all()

This is problematic because we cannot use array broadcasting with min in this way:

min(make_array(70, 73, 69), 72) #should be an error

---------------------------------------------------------------------------
ValueError                                Traceback (most recent call last)
Cell In[7], line 1
----> 1 min(make_array(70, 73, 69), 72) #should be an error

ValueError: The truth value of an array with more than one element is ambiguous. Use a.any() or a.all()

Instead, define our operation on a single value first:

def cut_off_at_72(x):
    """The smaller of x and 72"""
    return min(x, 72)

cut_off_at_72(62)

cut_off_at_72(72)

cut_off_at_72(78)

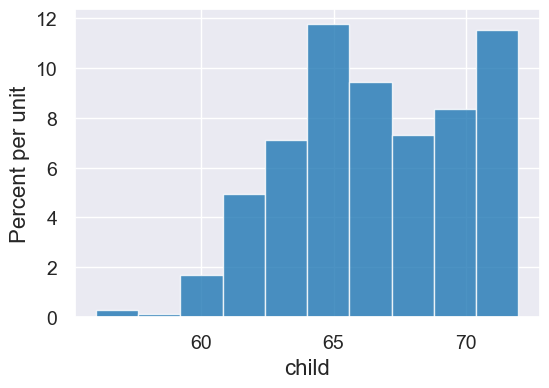
The table apply method can then apply such a function to every entry in a column.

cut_off = heights.apply(cut_off_at_72, 'child')
height2 = heights.with_columns('child', cut_off)

height2.hist('child')

Apply with multiple columns#

heights.show(6)

father	mother	child
78.5	67	73.2
78.5	67	69.2
78.5	67	69
78.5	67	69
75.5	66.5	73.5
75.5	66.5	72.5

... (928 rows omitted)

def average(x, y):
    """Compute the average of two values"""
    return (x + y) / 2

parent_avg = heights.apply(average, 'mother', 'father')
parent_avg.take(np.arange(0, 6))

array([72.75, 72.75, 72.75, 72.75, 71.  , 71.  ])

heights = heights.with_columns(
    'parent average', parent_avg
)
heights

father	mother	child	parent average
78.5	67	73.2	72.75
78.5	67	69.2	72.75
78.5	67	69	72.75
78.5	67	69	72.75
75.5	66.5	73.5	71
75.5	66.5	72.5	71
75.5	66.5	65.5	71
75.5	66.5	65.5	71
75	64	71	69.5
75	64	68	69.5

... (924 rows omitted)

heights.scatter('parent average', 'child')

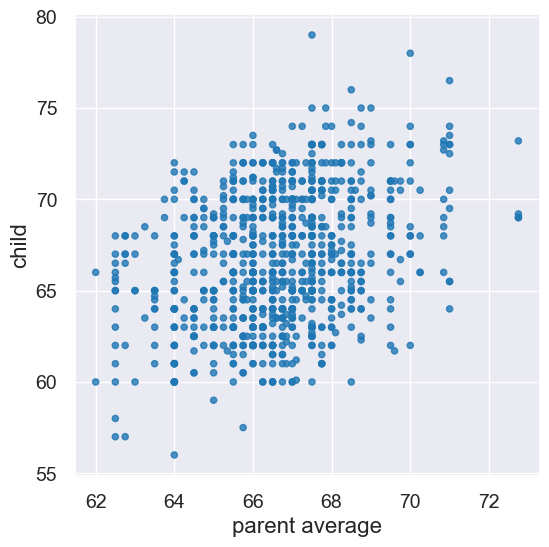
2. Predicting heights using functions and apply#

We’re following the example in Ch. 8.1.3

Think-pair-share: Suppose researchers encountered a new couple, similar to those in this dataset, and wondered how tall their child would be once their child grew up. What would be a good way to predict the child’s height, given that the parent average height was, say, 68 inches?

plot = heights.scatter('parent average', 'child')
plot.line(68, color='orange', linestyle='--', lw=2);

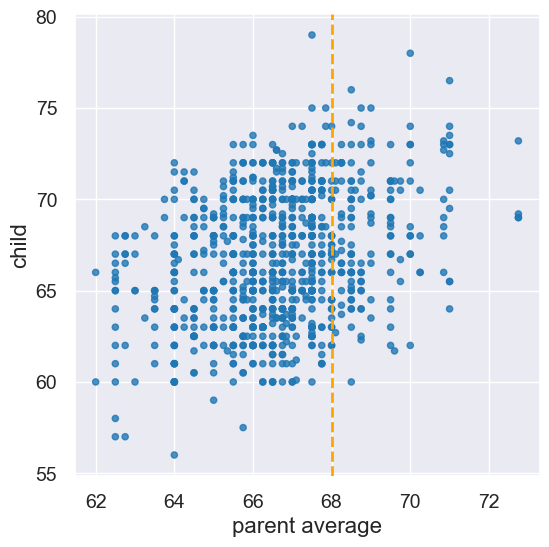
A: One initial approach would be to base the prediction on all observations (child, parent pairs) that are “close to” 68 inches for the parent.

Let’s take “close to” to mean within a half-inch
Let’s draw these with red lines

target_x_value = 68
close = 0.5

plot = heights.scatter('parent average', 'child')
plot.line(x=target_x_value - close, color='red', lw=1)
plot.line(x=target_x_value + close, color='red', lw=1)
plot.line(target_x_value, color='orange', linestyle='--', lw=2)
plot.dot(x=target_x_value, y=67.62, color='orange')

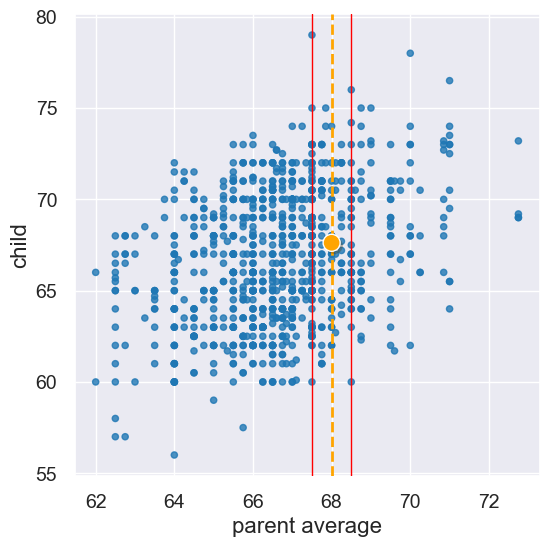
Let’s now identify all points within that red strip.

close_to_68 = heights.where('parent average', 
                            are.between(target_x_value - close, 
                                        target_x_value + close))
close_to_68

father	mother	child	parent average
74	62	74	68
74	62	70	68
74	62	68	68
74	62	67	68
74	62	67	68
74	62	66	68
74	62	63.5	68
74	62	63	68
74	61	65	67.5
73.2	63	62.7	68.1

... (175 rows omitted)

And take the average to make a prediction about the child.

np.average(close_to_68.column('child'))

67.62

Ooo! Let’s write a function to compute that child mean height for any parent average height

def predict_child(parent_avg_height):
    close = 0.5
    close_points = heights.where('parent average', 
                                 are.between(parent_avg_height - close, 
                                             parent_avg_height + close))
    return np.mean(close_points.column('child'))

predict_child(68)

67.62

predict_child(65)

65.83829787234043

Apply predict_child to all the parent averages.

predicted = heights.apply(predict_child, 'parent average')
predicted.take(np.arange(0,10))

array([70.1       , 70.1       , 70.1       , 70.1       , 70.41578947,
       70.41578947, 70.41578947, 70.41578947, 68.5025    , 68.5025    ])

Now, let’s extend this table with these new predictions.

height_pred = heights.with_columns('prediction', predicted)

height_pred.select('child', 'parent average', 'prediction').scatter('parent average')

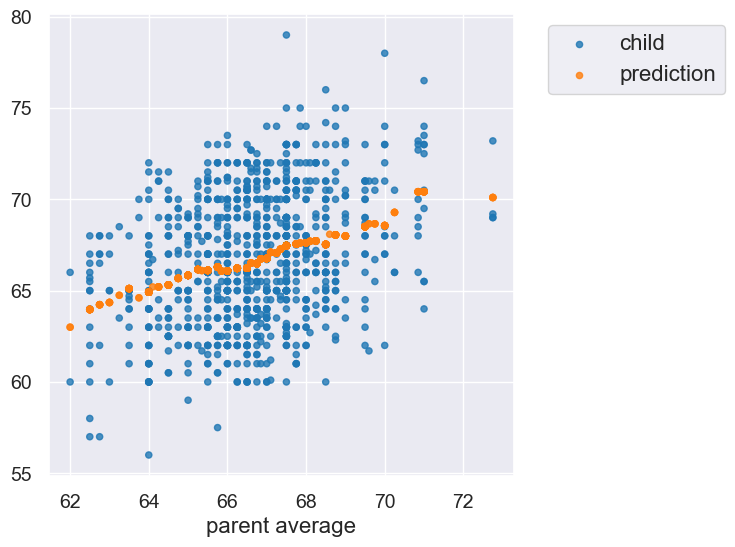
Preview: Throughout this course we’ll keep moving towards making our predictions better!

Extra: How close is close enough for prediction?#

The choice of say two heights are “close to” eachother if they are within a half-inch was a somewhat arbitrary choice. We chould have chosen other values instead. What would happen if we changed that constant to be 0.25, 1, 2, or 5?

This visualization demostrates the impact that choice has on our predictions. The visualize_predictions function plots the prediction for each child height using a window of parent average height +/- delta.

The following cell contains an interactive visualization. You won’t see the visualization on this web page, but you can view and interact with it if you run this notebook on our server here.

from functools import lru_cache as cache

@cache  # saves tables for each delta we compute to avoid recomputing.
def vary_range(delta):
    """Use a window of +/- delta when predicting child heights."""
    def predict_child(parent_avg_height):
        close_points = heights.where('parent average', 
                                     are.between(parent_avg_height - delta, 
                                                 parent_avg_height + delta))
        return np.mean(close_points.column('child'))

    predicted = heights.apply(predict_child, 'parent average')
    height_pred = heights.with_columns('prediction', predicted)
    return height_pred.select('child', 'parent average', 'prediction')

def visualize_predictions(delta = 0.5):
    predictions = vary_range(delta)
    predictions.scatter('parent average', s=50) # make dots a little bigger than usual
    
interact(visualize_predictions, delta = Choice(0,0.25, 0.5, 1, 3, 5, 10))

Here’s an animation that demostrates the impact that our choice of “close enough” has on our predictions. As you can see, if it’s very small, there is a lot of variability in the prediction. If it’s very large, the prediction can be pretty far off from the mean for a given height.

3. Groups with Scrabble#

Let’s load a table of 98 tiles from Scrabble. (We’ll exclude the two blank tiles from the full set of 100.)

scrabble_tiles = Table().read_table('data/scrabble_tiles.csv')
scrabble_tiles.sample(10)

Letter	Score	Vowel
I	1	Yes
L	1	No
O	1	Yes
P	3	No
P	3	No
B	3	No
T	1	No
E	1	Yes
I	1	Yes
U	1	Yes

We must often divide rows into groups according to some feature, and then compute a basic characteristic for each resulting group.

scrabble_tiles.group('Letter')

Letter	count
A	9
B	2
C	2
D	4
E	12
F	2
G	3
H	2
I	9
J	1

... (16 rows omitted)

scrabble_tiles.group('Vowel')

Vowel	count
No	56
Yes	42

scrabble_tiles.group('Vowel', sum)

Vowel	Letter sum	Score sum
No		145
Yes		42

Notes:

When we pass in a function to group that is not the default (e.g. sum), the name of that function is appended to the column name.
Some of the columns are empty because sum can only be applied to numerical (not categorial) variables. Our package is smart about this and leaves the columns empty (e.g. Letter sum).

scrabble_tiles.group('Vowel', max)

Vowel	Letter max	Score max
No	Z	10
Yes	U	1

Applying aggregation functions (e.g. max) to some columns (e.g. Letter) are not meaningful. That’s ok. But we’ll have to use our understanding about the dataset to ignore these aggregations.

Group multiple columns#

small_scrabble = scrabble_tiles.sample(10)
small_scrabble = small_scrabble.with_columns('Used', 
                                             make_array('Yes', 'Yes', 'Yes', 'No', 'No', 
                                                        'No', 'No', 'No', 'No', 'No'))
small_scrabble

Letter	Score	Vowel	Used
R	1	No	Yes
U	1	Yes	Yes
U	1	Yes	Yes
C	3	No	No
N	1	No	No
O	1	Yes	No
I	1	Yes	No
U	1	Yes	No
K	5	No	No
U	1	Yes	No

Q: How many vowels do I have left that I have not used?

small_scrabble.group(make_array('Vowel', 'Used'))

Vowel	Used	count
No	No	3
No	Yes	1
Yes	No	4
Yes	Yes	2

Q: What’s the total score of the non-vowels I have used and not used?

small_scrabble.group(make_array('Vowel', 'Used'), sum)

Vowel	Used	Score sum
No	No	9
No	Yes	1
Yes	No	4
Yes	Yes	2

4. Groups with heights#

heights_original.show(3)

family	father	mother	midparentHeight	children	childNum	gender	childHeight
1	78.5	67	75.43	4	1	male	73.2
1	78.5	67	75.43	4	2	female	69.2
1	78.5	67	75.43	4	3	female	69

... (931 rows omitted)

Q: How many children does each family have?

by_family = heights_original.group('family')
by_family.show(5)

family	count
1	4
10	1
100	3
101	4
102	6

... (200 rows omitted)

Let’s relabel based on what we know about this particular dataset (each row is a child).

by_family = by_family.relabeled("count", "number of children")

by_family.hist("number of children", bins=15)

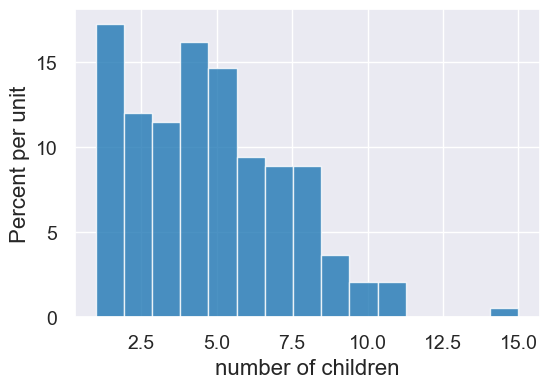
Q: Per family, what is the average height of the children?

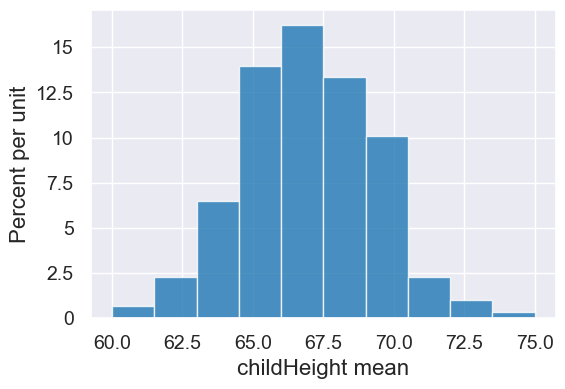
by_family = heights_original.select('family', 'childHeight').group('family', np.mean)
by_family.show(5)
by_family.hist('childHeight mean')

family	childHeight mean
1	70.1
10	65.5
100	70.7333
101	72.375
102	66.1667

... (200 rows omitted)

CSCI 104: Data Science and Computing for All

Groups

Contents

Groups#

1. Functions#

Apply#

Apply with multiple columns#

2. Predicting heights using functions and apply#

Extra: How close is close enough for prediction?#

3. Groups with Scrabble#

Group multiple columns#

4. Groups with heights#

Letter	Score	Vowel	Used
R	1	No	Yes
U	1	Yes	Yes
U	1	Yes	Yes
C	3	No	No
N	1	No	No
O	1	Yes	No
I	1	Yes	No
U	1	Yes	No
K	5	No	No
U	1	Yes	No

Letter	Score	Vowel	Used
R	1	No	Yes
U	1	Yes	Yes
U	1	Yes	Yes
C	3	No	No
N	1	No	No
O	1	Yes	No
I	1	Yes	No
U	1	Yes	No
K	5	No	No
U	1	Yes	No

CSCI 104: Data Science and Computing for All

Groups

Contents

Groups#

1. Functions#

Think-pair-share#

Apply#

Apply with multiple columns#

2. Predicting heights using functions and apply#

Extra: How close is close enough for prediction?#

3. Groups with Scrabble#

Group multiple columns#

4. Groups with heights#

Letter	Score	Vowel	Used
R	1	No	Yes
U	1	Yes	Yes
U	1	Yes	Yes
C	3	No	No
N	1	No	No
O	1	Yes	No
I	1	Yes	No
U	1	Yes	No
K	5	No	No
U	1	Yes	No