Hypothesis Testing and Statistical Significance
Contents
Hypothesis Testing and Statistical Significance#
from datascience import *
from cs104 import *
import numpy as np
%matplotlib inline
1. Midterm Scores#
Was Lab Section 3 graded differently than that other lab sections, or could their low average score be attributed to the random chance of the students assigned to that section?
scores = Table().read_table("data/scores_by_section.csv")
scores.group("Section")
| Section | count |
|---|---|
| 1 | 32 |
| 2 | 32 |
| 3 | 27 |
| 4 | 30 |
scores.group("Section", np.mean)
| Section | Midterm mean |
|---|---|
| 1 | 15.5938 |
| 2 | 15.125 |
| 3 | 13.1852 |
| 4 | 14.7667 |
Lab section 3’s observed average score on the midterm.
observed_scores = scores.where("Section", 3).column("Midterm")
observed_scores
array([20, 10, 20, 8, 22, 0, 15, 23, 23, 18, 15, 9, 20, 10, 0, 10, 22,
18, 4, 16, 7, 11, 11, 0, 16, 11, 17])
observed_average = np.mean(observed_scores)
observed_average
13.185185185185185
Number of students in Lab Section 3
observed_sample_size = scores.where("Section", 3).num_rows
observed_sample_size
27
Null hypothesis model: mean of the population
Null hypothesis restated: The mean in any sample should be close to the mean in the population (the whole class)
null_hypothesis_model_parameter = np.mean(scores.column("Midterm"))
null_hypothesis_model_parameter
14.727272727272727
Difference between Lab Section 3’s average midterm score and the average midterm score across all students.
observed_midterm_statistic = abs(observed_average - null_hypothesis_model_parameter)
observed_midterm_statistic
1.5420875420875415
Abstraction: Let’s create a function that calculates a statistic as the absolute difference between the mean of a sample and the mean of a population.
def statistic_abs_diff_means(sample, population):
"""Return the absolute difference in means between a sample and a population"""
return np.abs(np.mean(sample) - np.mean(population))
observed_midterm_statistic = statistic_abs_diff_means(observed_scores,
scores.column("Midterm"))
def sample_scores(sample_size):
# Note: we're using with_replacement=False here because we don't
# want to sample the same student's score twice.
return scores.sample(sample_size, with_replacement=False).column("Midterm")
sample_scores(observed_sample_size)
array([15, 16, 21, 21, 12, 16, 18, 13, 22, 15, 17, 21, 13, 17, 13, 22, 22,
11, 21, 20, 1, 11, 0, 8, 13, 18, 11])
def simulate_scores(observed_sample_size, num_trials):
simulated_midterm_statistics = make_array()
for i in np.arange(0, num_trials):
one_sample = sample_scores(observed_sample_size)
simulated_statistic = statistic_abs_diff_means(one_sample, scores.column("Midterm"))
simulated_midterm_statistics = np.append(simulated_midterm_statistics,
simulated_statistic)
return simulated_midterm_statistics
simulated_midterm_statistics = simulate_scores(observed_sample_size, 3000)
results = Table().with_columns("Statistic: abs(sample mean - population mean)",
simulated_midterm_statistics)
plot = results.hist(title="Empirical distribution of the \nsimulated statistic \nunder Null Hypothesis")
plot.dot(observed_midterm_statistic)
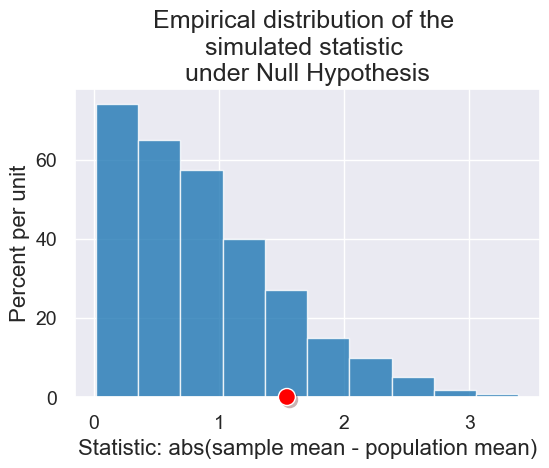
2. Calculating p-values#
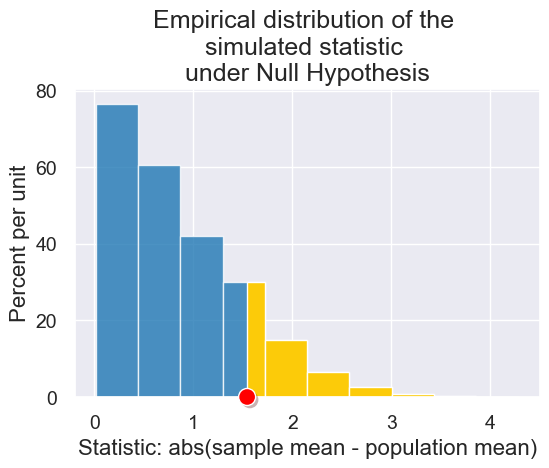
def plot_simulated_and_observed_statistics(simulated_statistics, observed_statistic):
"""
Plots the empirical distribution of the simulated statistics, along with
the observed data's statistic, highlighting the tail in yellow.
"""
results = Table().with_columns("Statistic: abs(sample mean - population mean)",
simulated_statistics)
plot = results.hist(left_end=observed_statistic, title="Empirical distribution of the \nsimulated statistic \nunder Null Hypothesis")
plot.dot(observed_statistic)
plot_simulated_and_observed_statistics(simulated_midterm_statistics, observed_midterm_statistic)
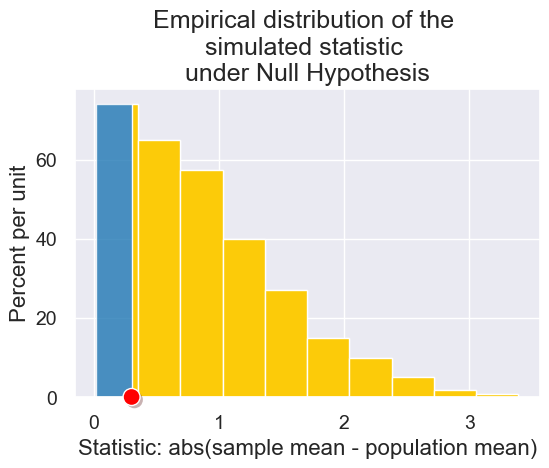
Supposed we observed other observed statistics.
plot_simulated_and_observed_statistics(simulated_midterm_statistics, 0.3)
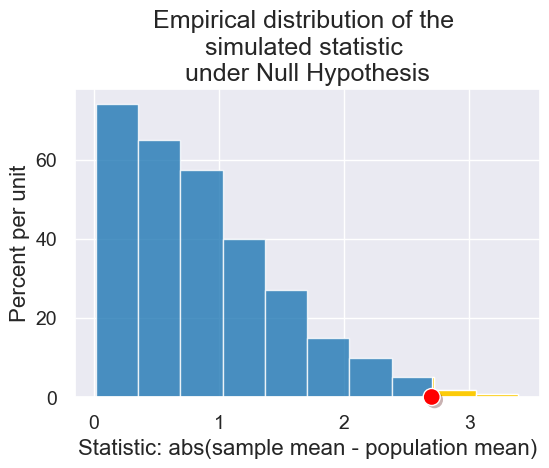
plot_simulated_and_observed_statistics(simulated_midterm_statistics, 2.7)
Calculating p-values: Let’s compute the proportion of the histogram that is colored yellow. This captures the proportion of the simulated samples under the null hypothesis that are more unlikely than the observed data.
simulated_midterm_statistics
array([2.28282828, 1.46801347, 0.93939394, ..., 0.57912458, 0.13468013,
1.71717172])
def calculate_pvalue(simulated_statistics, observed_statistic):
"""
Return the proportion of the simulated statistics that are greater than
or equal to the observed statistic
"""
return np.count_nonzero(simulated_statistics >= observed_statistic) / len(simulated_statistics)
calculate_pvalue(simulated_midterm_statistics, observed_midterm_statistic)
0.15433333333333332
Computing Percentiles
hw_scores = make_array( 31, 34, 36, 41, 43, 44, 45, 49, 51 )
percentile(50, hw_scores)
43
percentile(75, hw_scores)
45
results.hist()
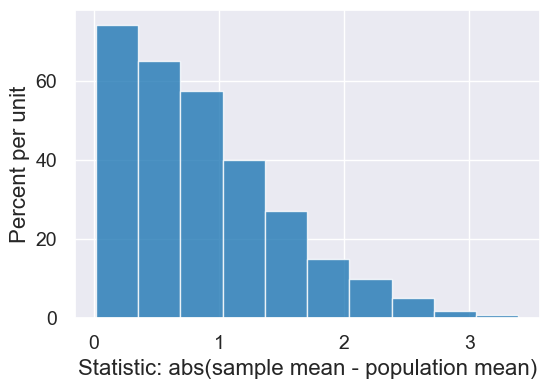
percetile_55 = percentile(55, simulated_midterm_statistics)
percetile_55
0.801346801346801
results.hist(left_end=percetile_55)
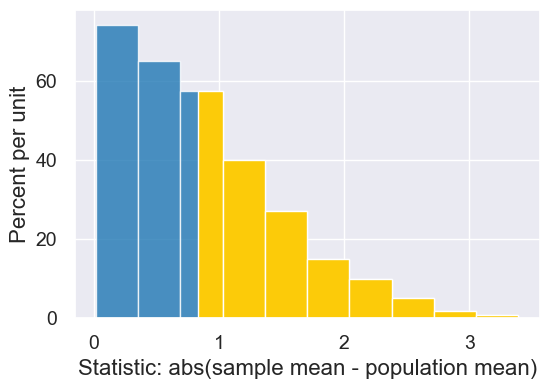
with Figure(1,4,figsize=(5.5,4)):
for percentile_k in make_array(50, 90, 95, 99):
simulated_midterm_percentile = percentile(percentile_k, simulated_midterm_statistics)
plot = results.hist(left_end=simulated_midterm_percentile, end_color="C9",
title = str(percentile_k)+'% of the distribution falls below '+str(np.round(simulated_midterm_percentile, 2)))
plot.line(x=simulated_midterm_percentile,color="purple", linestyle="dashed")

with Figure(1,2,figsize=(6,5)):
for percentile_k in make_array(95, 99):
simulated_midterm_percentile = percentile(percentile_k, simulated_midterm_statistics)
plot = results.hist(left_end=simulated_midterm_percentile, end_color="C9",
title = "p-value cutoff of " + str(100 - percentile_k) + "%")
plot.line(x=simulated_midterm_percentile,color="purple", linestyle="dashed")
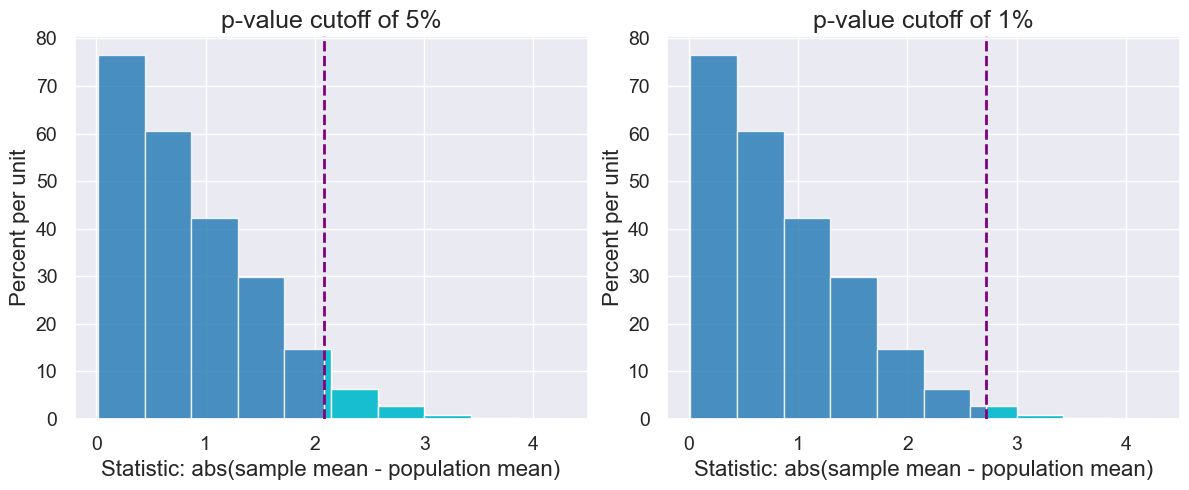
Let’s assume we are in our same set-up: our statistic is an absolute difference between the observed/simulated data and model parameters. We can then:
calculate the value of the statistic at the (conventional) 0.05 p-value and
put that statistic into our previous function
calculate_pvalue.The result in step 2 should be ~0.05!
statistic_at_five_percent_cutoff = percentile(100 - 5, simulated_midterm_statistics)
statistic_at_five_percent_cutoff
2.0875420875420865
calculate_pvalue(simulated_midterm_statistics, statistic_at_five_percent_cutoff)
0.050666666666666665
Let’s write a generic function for the value of the statistic to obtain a certain p-value.
def statistic_given_pvalue(pvalue, simulated_statistics):
"""
Return the value from the simulated statistic value for a specific p-value.
"""
return percentile(100 - pvalue, simulated_statistics)
statistic_given_pvalue(5, simulated_midterm_statistics)
2.0875420875420865
statistic_given_pvalue(1, simulated_midterm_statistics)
2.7171717171717162
3. Impact of Sample Size on p-value#
def visualize_p_value_and_sample_size(sample_size, p_cutoff):
simulated_midterm_statistics = make_array()
for i in np.arange(0, 2000):
one_sample = sample_scores(sample_size)
simulated_statistic = statistic_abs_diff_means(one_sample,
scores.column("Midterm"))
simulated_midterm_statistics = np.append(simulated_midterm_statistics,
simulated_statistic)
simulated_midterm_percentile = percentile(100 - p_cutoff,
simulated_midterm_statistics)
results = Table().with_columns("Statistic: abs(sample mean - class mean)",
simulated_midterm_statistics)
plot = results.hist(left_end=observed_midterm_statistic,bins=np.arange(0,6,0.2),
title = str(100 - p_cutoff)+'% of the distribution falls below '+str(np.round(simulated_midterm_percentile, 2)) + "\nSample size = "+str(sample_size),
xlim = (0,5),
ylim = (0,1.5))
plot.dot(observed_midterm_statistic)
plot.line(x=simulated_midterm_percentile,color="purple", linestyle="dashed")
The following cell contains an interactive visualization. Run this notebook on our server here to view it.
interact(visualize_p_value_and_sample_size,
sample_size=Slider(10,100),
p_cutoff=Slider(1,100))
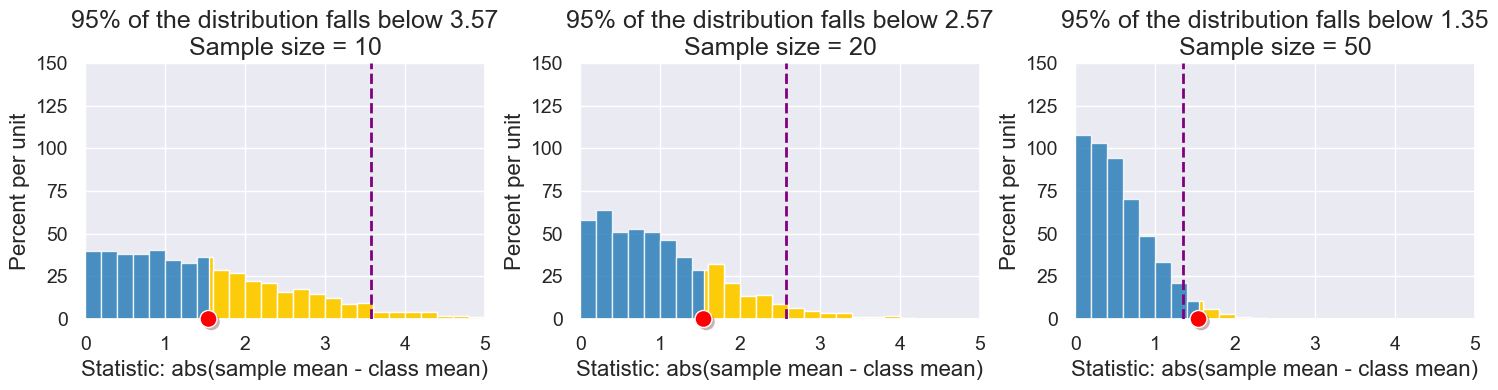
Takeaway: If we have a larger sample size, the value of the test statistic to give the same p-value cut-off is less. In other words, with a larger sample size we don’t have to see as larger of extreme values to have the same statistical significance (the burden of proof that it’s not by chance is lower).

