Inference with Statistics#

from datascience import *
from cs104 import *
import numpy as np
%matplotlib inline

1. Snoopy’s Fleet#

We will create a simulation for the empirical distribution of our chosen statistic.

At true inference time, we do not know N. However, let’s create N now so that we can evaluate how “good” our chosen models and statistics could be.

N = 300

population = np.arange(1, N+1)

Suppose we didn’t know N. Then all we could do is observe samples of planes flying overhead.

We’ll use our model assumption: Plane numbers are uniform random sample drawn with replacement from 1 to N.

def sample_plane_fleet(sample_size):
    return np.random.choice(population, sample_size)

sample = sample_plane_fleet(10)
sample

array([159, 261, 194, 203, 108, 207, 190, 195, 153, 237])

Option 1: Sample Statistic is the max plane number#

Let’s choose a stastic as the max of as sample. Luckily, max is simple and we don’t have to write a new function here. We can use Python’s built-in function!

max(sample)

Let’s put this all together using our simulation algorithm.

sample_size = 10
num_trials = 1000

all_outcomes = simulate_sample_statistic(sample_plane_fleet, sample_size, 
                                         max, num_trials)

results = Table().with_columns("Statistic Option 1: Max Sample", all_outcomes)
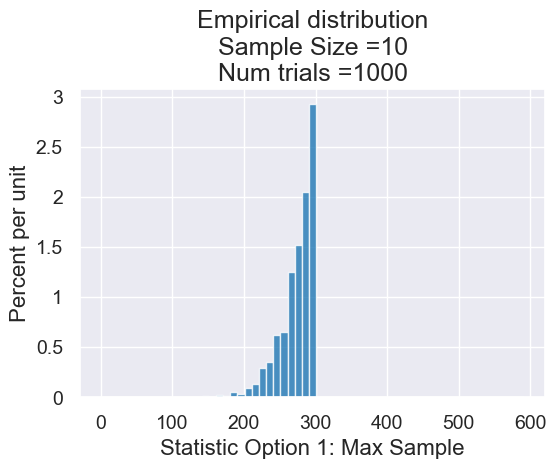
plot = results.hist(bins=np.arange(1, 2 * N, 10))
plot.set_title("Empirical distribution\n"+
               "Sample Size ="+str(sample_size)+ 
               "\nNum trials ="+str(num_trials))

../_images/17-inference-with-statistics_16_0.png

Let’s generalize a bit and create function that takes the statistic and runs the whole experiment.

Option 2: Sample Statistic is Twice the Mean#

Let’s generalize a bit and create function that takes the statistic and runs the whole experiment

def planes_empirical_statistic_distribution(sample_size, compute_sample_statistic, num_trials):
    """
    Simulates multiple trials of a statistic on our simulated fleet of N planes 
    
    Inputs 
        - sample_size: number of planes we see in our sample
        - compute_sample_statistic: a function that takes an array 
            and returns a summary statistic (e.g. max)
        - num_trials: number of simulation trials 
        
    Output 
        Histogram of the results 
    """
    all_outcomes = simulate_sample_statistic(sample_plane_fleet, sample_size, 
                                             compute_sample_statistic, num_trials)
        
    results = Table().with_columns('Empirical Distribution, Statistic: ' + compute_sample_statistic.__name__, 
                                   all_outcomes)
    plot = results.hist(bins=np.arange(1, 2 * N, 10))
    plot.set_title("Empirical distribution\n"+
               "Sample Size ="+str(sample_size)+ 
               "\nNum trials ="+str(num_trials))
    
    # Red line is the True N    
    plot.line(x=N, color='r', linestyle='--')    

planes_empirical_statistic_distribution(10, max, 1000)

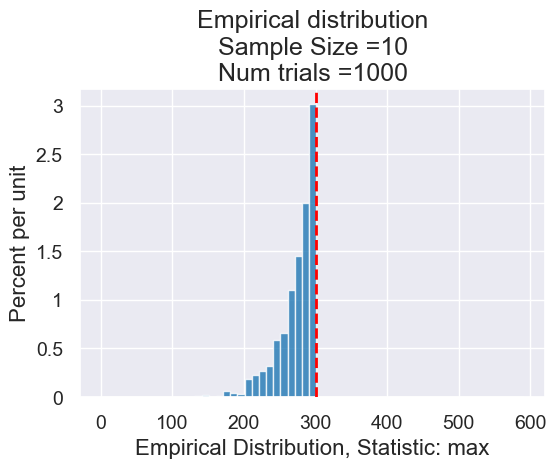
../_images/17-inference-with-statistics_21_0.png

Our second option for the statistic:

def twice_mean(sample):
    """Twice the sample mean"""
    return 2 * np.mean(sample)

planes_empirical_statistic_distribution(10, twice_mean, 1000)    

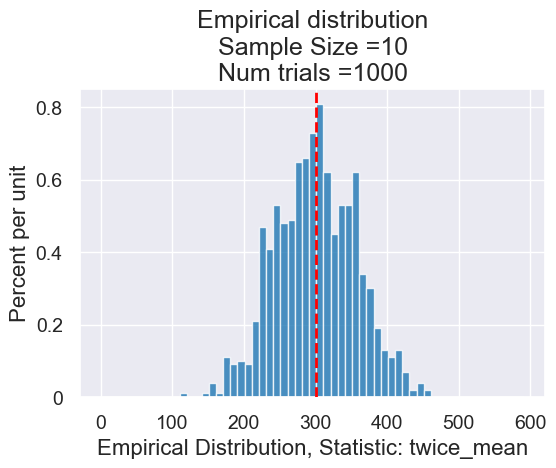
../_images/17-inference-with-statistics_23_0.png

2.Effects of Sample Size and Simulation Rounds#

First interaction: Let’s just look at the number of trials just for our twice mean statistic with everything else held constant.

interact(planes_empirical_statistic_distribution,
         sample_size=Fixed(20), 
         compute_sample_statistic=Fixed(twice_mean),
         num_trials=Slider(1, 20010, 10))

num_trials

Here are a few sample distrubtions with different numbers of trials.

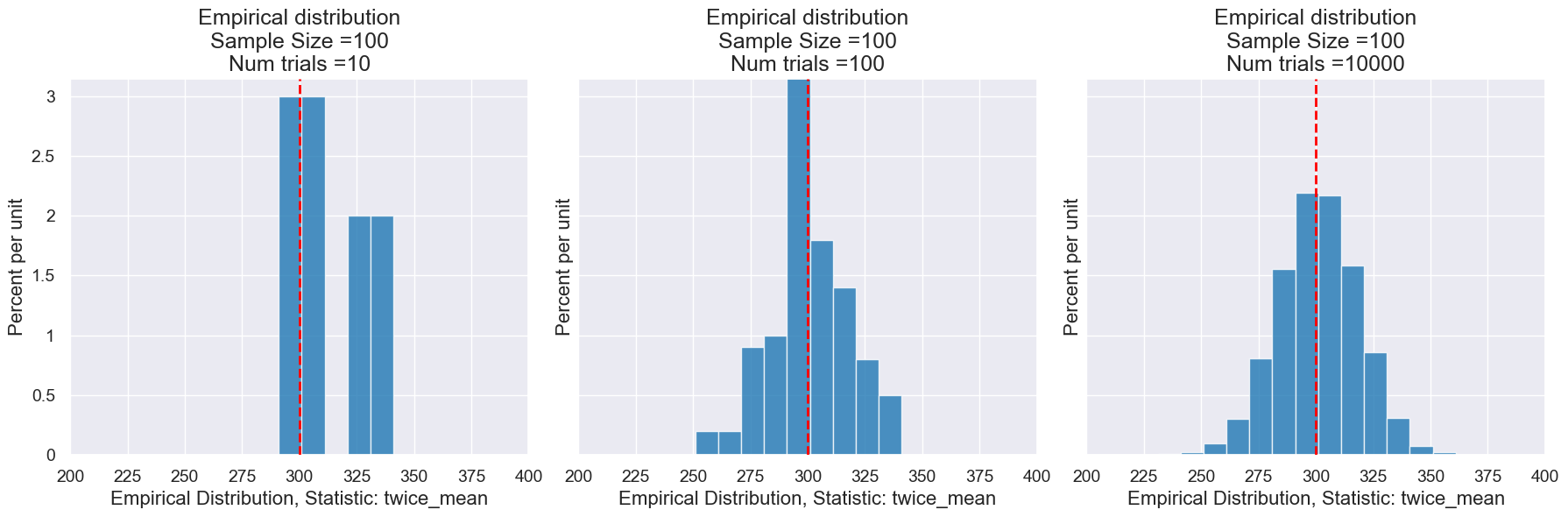
../_images/17-inference-with-statistics_29_0.png

We can also examinge the impact of changing the sample size and N using the following function.

def visualize_distributions(N, sample_size, num_trials):
    """A single function to run our simulation for a given N, sample_size, and num_trials."""
    import matplotlib.pyplot as plt
    
    population = np.arange(1, N+1)
    
    # Builds up our outcomes table one row at a time.  We do this to ensure
    # we can apply both statistics to the same samples.
    outcomes_table = Table(["Max", "2*Mean"])
    
    for i in np.arange(num_trials):
        sample = np.random.choice(population, sample_size)
        outcomes_table.append(make_array(max(sample), 2 * np.mean(sample)))
        
    plot = outcomes_table.hist(bins=np.arange(N/2, 3*N/2, 2))
    plot.set_title("Empirical distribution (N="+str(N)+")\n"+
               "Sample size ="+str(sample_size)+ 
               "\nNum trials ="+str(num_trials))
    # Red line is the True N
    plot.line(x=N, color='r', linestyle='--')

interact(visualize_distributions, 
         N=Slider(100, 450, 50), 
         sample_size=Slider(10, 101, 1), 
         num_trials=Slider(10, 10100, 100))

sample_size

num_trials

Here’s a visualization of how sample size impacts the distribution of our statistic for random samples.

Here’s a visualization of how the number of trials impacts the distribution of our statistic for random samples.

Here’s a visualization of how the parameter N impacts the distribution of our statistic for random samples.

3. Mendel and Pea Flowers#

Looking ahead, we know we’ll be using our simulate sample statistc! So let’s build and check all these pieces.

simulate_sample_statistic(make_sample,
   sample_size,
   compute_statistic,
   num_trials)

Observed sample: In Mendel’s one sample (his own garden), he had 929 second new generation pea plants, of which 709 had purple flowers. We compute the percent purple he observed:

observed_sample_size = 929
observed_purples = 709 / observed_sample_size * 100
observed_purples

76.31862217438106

Model: Mendel hypothesized (based on his preliminary theories of genetics) that he should have gotten 75% purple and 25% white.

hypothesized_purple_proportion = 0.75
hypothesized_proportions = make_array(hypothesized_purple_proportion, 
                                      1 - hypothesized_purple_proportion) 
hypothesized_proportions

array([0.75, 0.25])

In the Python library reference, we see can use the function sample_proportions(sample_size, model_proportions).

sample = sample_proportions(observed_sample_size, hypothesized_proportions)
sample

array([0.7664155, 0.2335845])

Let’s put it into a function.

def flowers_make_sample(sample_size): 
    """
    Return the percents of purple flowers and white flowers in an array
    """
    hypothesized_purple_proportion = 0.75
    hypothesized_proportions = make_array(hypothesized_purple_proportion, 
                                          1 - hypothesized_purple_proportion) 
    sample = 100 * sample_proportions(sample_size, hypothesized_proportions)
    return sample

flowers_make_sample(observed_sample_size)

array([75.67276642, 24.32723358])

Each item in the array corresponds to the proportion of times it was sampled out of sample_size times. So the proportion purple is

def stat_percent_purple(sample): 
    return sample.item(0)

stat_percent_purple(sample)

0.7664155005382132

Now let’s use our function simulate_sample_statistic.

num_trials = 1000

all_outcomes = simulate_sample_statistic(flowers_make_sample, observed_sample_size,
                                         stat_percent_purple, num_trials)

results = Table().with_column('Percent purple flowers', all_outcomes)
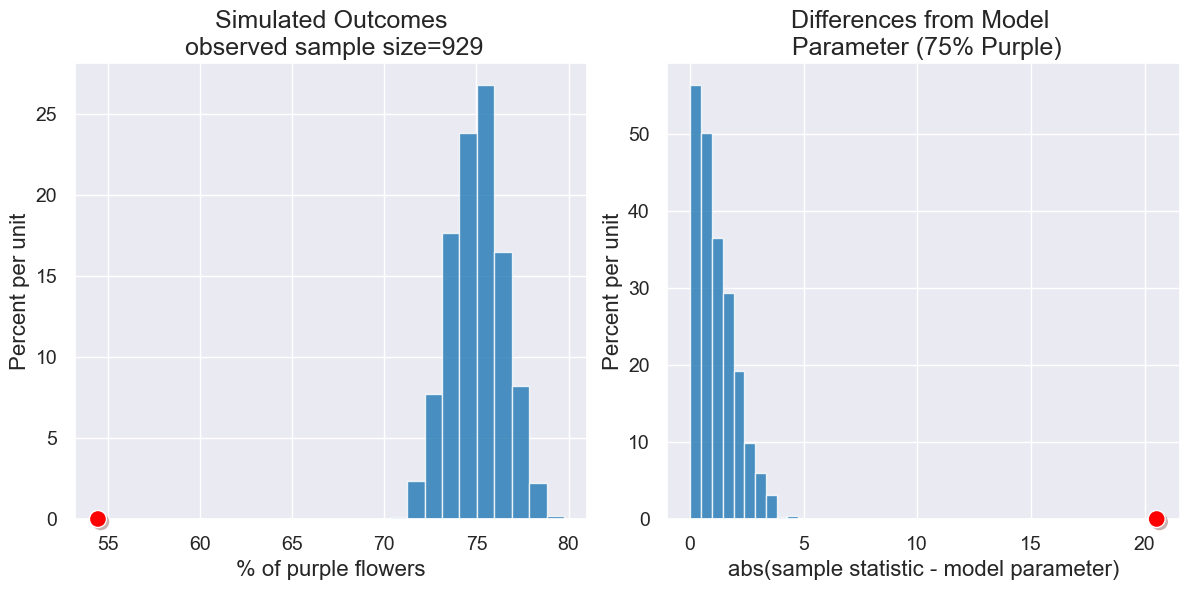
results.hist(title = 'Simulated Outcomes\n observed sample size=' + str(observed_sample_size))

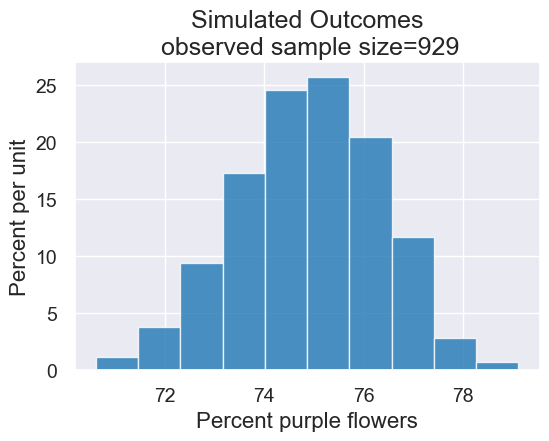
../_images/17-inference-with-statistics_55_0.png

Connecting these pieces together:

In Mendel’s model, he hypothesized getting purple flowers was like flipping a biased coin and getting heads 75% of the time.
We simulated outcomes under this hypothesis.
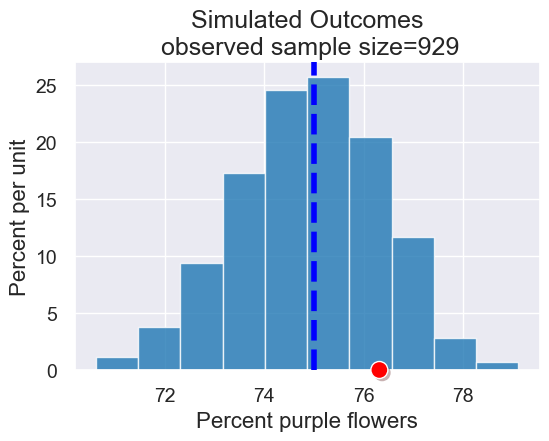
Now let’s check if the observed data (that there were 76.3% purple flowers in one sample, Mendel’s own garden) “fits” with the simulated outcomes under the model

plot = results.hist(title = 'Simulated Outcomes\n observed sample size=' + str(observed_sample_size))
plot.line(x=75,lw=4,linestyle="dashed")
plot.dot(observed_purples)

../_images/17-inference-with-statistics_57_0.png

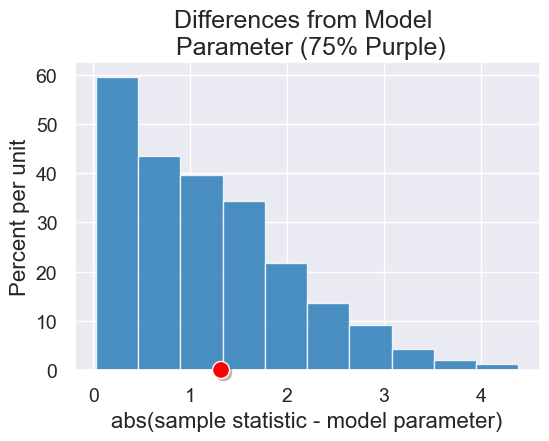
differences_from_model = Table().with_column('abs(sample statistic - model parameter)', 
                                             abs(all_outcomes - 75))

diff_plot = differences_from_model.hist(title = 'Differences from Model \n Parameter (75% Purple)')
diff_plot.dot(abs(observed_purples - 75))

../_images/17-inference-with-statistics_58_0.png

Once again, let’s use computation to abstract away the variables that we have the power to change, and the parts of the code that never change. Here is a new function to do that.

def pea_plants_simulation(observed_sample_size, observed_purples_count, 
                          hypothesized_purple_percent, num_trials): 
    """
    Parameters:
        - observed_sample_size: number of plants in our experiment
        - observed_purples_count: count of plants in our experiment w/ purple flowers
        - hypothesized_purple_proportion: our model parameter (hypothesis for 
              proportion of plants will w/ purple flowers).
        - num_trials: number of simulation rounds to run
    Outputs two plots:
        - Empirical distribution of the percent of plants w/ purple flowers 
          from our simulation trials
        - Empirical distribution of how far off each trial was from our hypothesized model
    """
    
    observed_purples = 100 * observed_purples_count / observed_sample_size
    hypothesized_proportions = make_array(hypothesized_purple_percent/100, 
                                          1 - hypothesized_purple_percent/100)
    
    assert 0 <= hypothesized_proportions[0] <= 1, str(hypothesized_proportions)
    assert 0 <= hypothesized_proportions[1] <= 1, str(hypothesized_proportions)
    
    all_outcomes = make_array()
    for i in np.arange(0, num_trials):
        simulated_sample = 100 * sample_proportions(observed_sample_size, hypothesized_proportions)
        outcome = simulated_sample.item(0)
        all_outcomes = np.append(all_outcomes, outcome)
    
    #plots
    with Figure(1,2):
        percent_purple = Table().with_column('% of purple flowers', all_outcomes)
        pp_plot = percent_purple.hist(title='Simulated Outcomes\n observed sample size=' + str(observed_sample_size))
        pp_plot.dot(observed_purples)

        distance_from_model = Table().with_column('abs(sample statistic - model parameter)', 
                                                  abs(all_outcomes - hypothesized_purple_percent))
        dist_plot = distance_from_model.hist(title='Differences from Model \n Parameter (' + str(hypothesized_purple_percent) + '% Purple)')
        dist_plot.dot(abs(observed_purples - hypothesized_purple_percent))

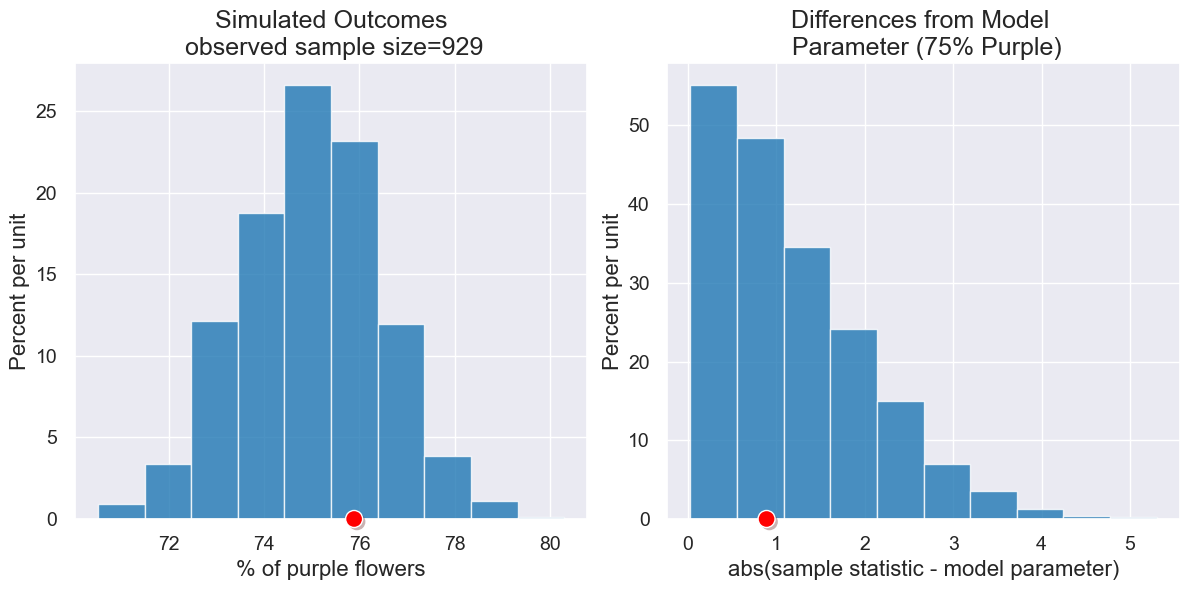
Here is a scenario to match Mendel’s garden. 705 out of 929 plants had purple flowers, and he proposed 75% should be purple.

pea_plants_simulation(929, 705, 75, 1000)

../_images/17-inference-with-statistics_62_0.png

Here is a different scenario. Suppose only 506 out of 929 plants had purple flowers, and but our model indicates that 75% should be purple.

pea_plants_simulation(929, 506, 75, 1000)

../_images/17-inference-with-statistics_64_0.png

interact(pea_plants_simulation,  
         observed_sample_size = Fixed(929), 
         observed_purples_count = Slider(0,929), 
         hypothesized_purple_percent = Slider(0,100,1),
         num_trials=Slider(10, 5000, 100))

#
#
#

---------------------------------------------------------------------------
AssertionError                            Traceback (most recent call last)
Cell In[36], line 1
----> 1 interact(pea_plants_simulation,  
      2          observed_sample_size = Fixed(929), 
      3          observed_purples_count = Slider(0,929), 
      4          hypothesized_purple_percent = Slider(0,100,1),
      5          num_trials=Slider(10, 5000, 100))
      7 #
      8 #
      9 #

Cell In[35], line 2, in interact(f, **kwargs)
      1 def interact(f, **kwargs):
----> 2     return html_interact(f, **kwargs)

    [... skipping hidden 6 frame]

Cell In[32], line 20, in pea_plants_simulation(observed_sample_size, observed_purples_count, hypothesized_purple_percent, num_trials)
     16 observed_purples = 100 * observed_purples_count / observed_sample_size
     17 hypothesized_proportions = make_array(hypothesized_purple_percent/100, 
     18                                       1 - hypothesized_purple_percent/100)
---> 20 assert 0 <= hypothesized_proportions[0] <= 1, str(hypothesized_proportions)
     21 assert 0 <= hypothesized_proportions[1] <= 1, str(hypothesized_proportions)
     23 all_outcomes = make_array()

AssertionError: [ 1.28 -0.28]

CSCI 104: Data Science and Computing for All

Inference with Statistics