| Computing Follow(N) |

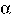 1 M R
1 M R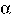 2,
then Follow(M) must contain the first symbols that might appear in strings
derived from R. In addition, if R derives the empty string, then the first symbols
that might be derived from
2,
then Follow(M) must contain the first symbols that might appear in strings
derived from R. In addition, if R derives the empty string, then the first symbols
that might be derived from 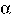 2 will be in Follow(M).
2 will be in Follow(M).
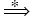
 .
.
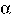
 (Vn U Vt)*
we define First(
(Vn U Vt)*
we define First(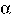 ) to be the set of terminals that
might appear as the first symbol in a string derived from
) to be the set of terminals that
might appear as the first symbol in a string derived from
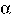 . First(
. First(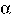 ) will include
) will include  if
if
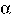
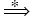
 . Thus,
. Thus,
First() = { a
Vt |
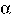
a
, for some
( Vn U Vt )* } U {
if
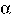
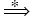
}

 .
.
 (Vt U Vn)
(Vt U Vn)
First( x )FirstSet[ x ]
 } for all nullable
non-terminals and to { } for all other non-terminals.
} for all nullable
non-terminals and to { } for all other non-terminals.
 t
t 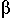 add
t to FirstSet[ N ].
add
t to FirstSet[ N ].

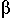 ,
write
,
write 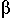 as
as 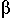 =
= 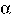
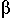 '
where
'
where
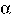 is a string of nullable non-terminals,
and
is a string of nullable non-terminals,
and 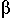 ' is either the
' is either the  or a string of terminals
and non-terminals beginning with a non-nullable symbol we will
call M.
or a string of terminals
and non-terminals beginning with a non-nullable symbol we will
call M.

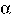
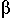 '
'

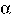 , add
(FirstSet[ x ] -
, add
(FirstSet[ x ] -  ) to FirstSet[ N ].
) to FirstSet[ N ].
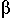 ' =
' =  then
add
then
add  to
FirstSet[ N ] otherwise add
(FirstSet[ M ] -
to
FirstSet[ N ] otherwise add
(FirstSet[ M ] -  ) to FirstSet[ N ].
) to FirstSet[ N ].
S
 A B C
A B C | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
A
 a | CB
a | CB | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
B
 C | A d |
C | A d |  | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
C
 f |
f | 
|
 B C, then implies
A is nullable.
B C, then implies
A is nullable.
 A B C implies S is
nullable.
A B C implies S is
nullable.
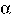 | 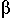 | |
S

| A B C | |
A

| a | |
A

| CB | |
B

| C | |
B

| A | d |
B

|  | |
C

| f | |
C

| 
|
| S | A | B | C | a | d | f |
{  } } |
{  , a } , a } |
{  } } |
{  , f } , f } | { a } | { d } | { f } |
| { } | { } | { } | { } | { a } | { d } | { f } |
|
{ } | { } | { } | { } | { a } | { d } | { f } |
|
{ } | { } | { } | { } | { a } | { d } | { f } |
Mthen Follow(N) must contains First(
N
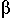 ) . If
) . If 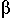 is nullable, then Follow(N) must also
contain Follow(M). These observations are enough to give us
an approximation algorithm for computing Follow. See the books
on reserve for details.
is nullable, then Follow(N) must also
contain Follow(M). These observations are enough to give us
an approximation algorithm for computing Follow. See the books
on reserve for details.
| Computing Follow(N) |