SLR(1) parsing

SLR(1) parsing

1. Consider the grammar

   < S > a < S > b < S >  | 

2. If we build the LR(0) machine for this grammar, we discover that it is not an LR(0) grammar because several states contain shift/reduce conflicts.
   • The initial state is composed of the items:

     [ < S' > . < S > $ ]
     [ < S > . a < S > b < S > ]
     [ < S > . ]

   • Starting from the initial state on input "a" we reach the the state:

     [ < S > a . < S > b < S > ]
     [ < S > . a < S > b < S > ]
     [ < S > . ]

   We can use this machine anyway, if we are willing to look ahead a bit.

   • In all the sentential forms you can generate from the grammar an "a" will never directly follows and S.
   • As a result, in either of the states shown, choosing to reduce when the next input is an "a" would definitely lead to a dead end.
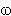3. In general, suppose that we find that after reading some prefix ₁ of an input 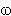₁ x 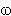₂ we end up in a state that contains a reduce item [ N . ] which conflicts with some other item.
   • If we decide to reduce using the production in this item, we are basically assuming that

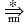
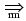
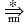
     S N x ₂ x _{2 1} x ₂

   • That is, we are assuming that there is some sentential form in which an x can follow an N.
4. We can give the set of symbols that might appear after a non-terminal a name:

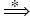
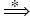
   Follow( N ) = { x V_t  | A N x } U { if S N }

5. Given the notion of the "follow" set, we can illustrate the use of look-ahead in LR parsing, by considering the simplest form of look-ahead LR parsing -- SLR(1) parsing (that's S for simple).
6. For the grammar considered above, a is not in Follow(S). So, we should never reduce using the production < S > if the next "input" symbol is a. Therefore, the three states with LR(0) conflicts really don't have conflicts at all.
7. In general, we will say that a set of LR(0) items contains an SLR(1) conflict if either:
   1. It contains two reduce items [ N ₁ . ] and [ M ₂ . ] such that the intersection of Follow(N) and Follow(M) is non-empty, or
   2. It contains a reduce item [ N ₁ . ] and a shift item [ M ₂ . x ₂ ] such that x Follow(N).
8. If the LR(0) machine for a grammar G contains no states with SLR(1) conflicts we say that G is an SLR(1) grammar.
9. An SLR(1) parser for an SLR(1) grammar G behaves as follows in state when the next input symbol is "x":
   • reduce using production N if [ N . ] , and x Follow(N).
   • shift in next input if contains one or more items of the form [ N 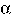. x ].
   • error otherwise.

SLR(1) parsing