| About this closure stuff... |
 )
)
 ' equal to
' equal to  .
.

 1 . M
1 . M  2 ]
2 ]

 '
such that M
'
such that M

 3
3  P and
[ M
P and
[ M
 .
.  3 ]
3 ] 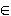
 ' add
[M
' add
[M
 .
.  3 ] to
3 ] to  '.
'.
 ) is valid for
) is valid for  using an argument based on showing that the claim that execution of the
loop body preserves the "invariant" that all items in
using an argument based on showing that the claim that execution of the
loop body preserves the "invariant" that all items in  ' are valid for
' are valid for  .
.
 are assumed valid for
are assumed valid for  , so the invariant will be true
when the loop begins to execute..
, so the invariant will be true
when the loop begins to execute..
 ' are valid for
' are valid for  and
let [ M
and
let [ M
 .
.  3 ] be
the item added during an execution of the loop body. The addition of this item implies
that some item of the form [ N
3 ] be
the item added during an execution of the loop body. The addition of this item implies
that some item of the form [ N

 1 . M
1 . M  2 ]
must have already been in
2 ]
must have already been in  '. By the assumption that the invariant
holds at the beginning of each execution of the loop body,
this item must be valid for
'. By the assumption that the invariant
holds at the beginning of each execution of the loop body,
this item must be valid for
 . Accordingly, there must be some derivation:
. Accordingly, there must be some derivation:
S'with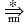
N
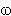
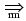
1 M
2
 =
= 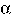
 1.
Assuming the grammar has no useless non-terminals, it must
be possible to derive some string of terminals,
1.
Assuming the grammar has no useless non-terminals, it must
be possible to derive some string of terminals, 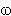 ' from
' from
 2. Thus, there is a derivation:
2. Thus, there is a derivation:
S'The existence of this derivation implies that the item [ M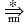
N
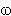
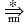
1 M
'
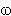
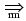
1
3
'
 .
.  3 ] is valid for
3 ] is valid for  . Therefore, adding
this item to
. Therefore, adding
this item to  ' preserves the invariant.
' preserves the invariant.
 . The basis step is so simple that we will look
at the induction step first:
. The basis step is so simple that we will look
at the induction step first:
 x
such that
x
such that  is of length n and x is a single symbol.
is of length n and x is a single symbol.
Suppose that [ N

 1 x .
1 x .  2 ] is an item
in
2 ] is an item
in 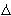 (
(  0,
0,  x ). The fact that this item is
in this set implies that the item
[ N
x ). The fact that this item is
in this set implies that the item
[ N

 1 . x
1 . x  2 ] must be in
2 ] must be in
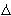 (
(  0,
0,  ). This, together with our inductive
assumption implies that [ N
). This, together with our inductive
assumption implies that [ N

 1 . x
1 . x  2 ]
must be valid for
2 ]
must be valid for  . Therefore, there exists a
derivation:
. Therefore, there exists a
derivation:
S'with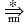
N
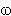
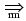
1 x
2
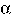
 1 =
1 =  . This, however implies that
[ N
. This, however implies that
[ N

 1 x .
1 x .  2 ] is indeed valid for
2 ] is indeed valid for  x.
x.
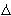 (
(  0, eps) is
[ S'
0, eps) is
[ S'
 . S]. The derivation
S'
. S]. The derivation
S'
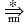 S'
S'
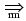 S
shows that this item is valid for eps.
S
shows that this item is valid for eps.
| About this closure stuff... |