About this closure stuff...

About this closure stuff...

1. Recall the definition for the closure of a set of LR(0) items:

   closure

   Given a set of LR(0) items for a grammar G with productions P, we define closure() to be the smallest set of LR(0) items such that:

   1. closure()
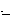
   2. if [N_{1 1} . N_{2 2}] closure() and N_{2 3} P then [N₂ . ₃] closure()

2. When we build an LR(0) machine we use the following algorithm to compute closures:
   • An algorithm to compute closure( )
     1. set ' equal to .
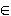
     2. while there is some [ N ₁ . M ₂ ] ' such that M ₃ P and [ M . ₃ ] ' add [M . ₃ ] to '.
3. How can we prove that the sets described by the definition and produced by the algorithm are the same?

   By identifying the invariant of the loop. Namely:

   At the beginning (and end) of each iteration of step (b), ' is a subset of the closure of .

   • This is clearly true before the first iteration.
   • If it is true before any subsequent iteration, then the item [ M . ₃ ] that the iteration will add must also be a member of closure( ) by the definition of closure.

   These facts establish that ' will always be a subset of closure( ). If the loop terminates, then we know that ' must contain closure( ) and therefore ' = closure( ). Luckily, the loop must terminate since there are only a finite number of LR(0) items that step (b) could add to '.

About this closure stuff...