| Constructing the LR(0) Machine for a Grammar |
 .
.
 .
.
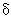 :
:  x
x 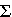 ->
->  .
.
 called the set of final
states.
called the set of final
states.
 0 of
0 of  called the initial state.
called the initial state.
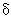 to strings over the input
alphabet. In particular, we can define
to strings over the input
alphabet. In particular, we can define
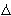 :
:  x
x 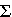 * ->
* ->  recursively as
recursively as
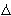 (
(  ,
,  ) =
) = 
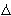 (
(  ,
, 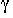 x ) =
x ) = 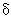 (
( 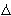 (
(  ,
, 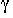 ), x )
), x )
{* |
(
0,
)
F }
Of course, we need a few more definitions:
goto(, x ) = { [ N

1 x .
2 ] | [ N

1 . x
2 ]
}
 of LR(0) items for a grammar G with
productions P, we define closure(
of LR(0) items for a grammar G with
productions P, we define closure( ) to be the smallest
set of LR(0) items such that:
) to be the smallest
set of LR(0) items such that:
 )
) 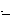


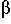 1 . N2
1 . N2 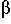 2]
2]
 closure(
closure( )
and N2
)
and N2

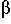 3
3  P
then
[N2
P
then
[N2
 .
. 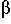 3]
3]  closure(
closure( )
)
 )
)
 ' equal to
' equal to  .
.

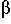 1 . M
1 . M 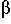 2 ]
2 ]

 '
such that M
'
such that M

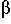 3
3  P and
[ M
P and
[ M
 .
. 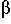 3 ]
3 ] 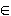
 ' add
[M
' add
[M
 .
. 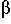 3 ] to
3 ] to  '.
'.
 S $ is added to the set of
productions (The $ just stands for end-of-input). The definition
of the LR(0) machine is:
S $ is added to the set of
productions (The $ just stands for end-of-input). The definition
of the LR(0) machine is:
 of states of the machine be the set of
all sets of LR(0) items for G.
of states of the machine be the set of
all sets of LR(0) items for G.
closure ( {[ S'. S $]} )
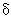 :
:  x (Vn U Vt) ->
x (Vn U Vt) ->  be
defined by:
be
defined by:
(
,x) = closure(goto(
,x))
| < S` > |
 < S > $
< S > $ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| < S > |
 < S > a < S > b | c
< S > a < S > b | c
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
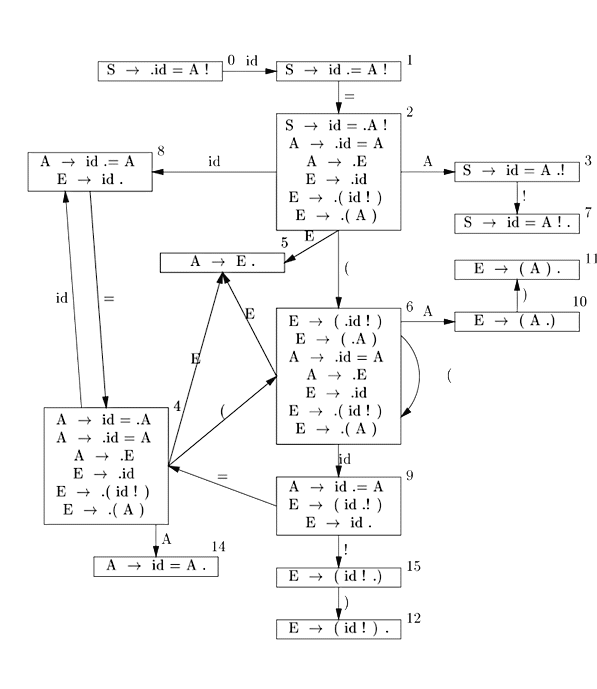
| Constructing the LR(0) Machine for a Grammar |