| How Lex Works |
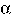 +. Any such expression
can be rewritten as
+. Any such expression
can be rewritten as 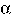 (
(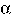 *). Accordingly, if we figure out how
to handle concatenation and *, we don't have to worry about +. We can just rewrite
any expression that uses + before we start trying to build an FSA.
*). Accordingly, if we figure out how
to handle concatenation and *, we don't have to worry about +. We can just rewrite
any expression that uses + before we start trying to build an FSA.
 .
.
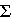 .
.
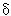 :
:  x
x  ->
->  .
.
 called the set of final
states.
called the set of final
states.
 0 of
0 of  called the initial state.
called the initial state.
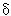 would have
been undefined we will define its result to be the error state.
would have
been undefined we will define its result to be the error state.
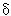 to strings over the input
alphabet. In particular, we can define
to strings over the input
alphabet. In particular, we can define
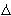 :
:  x
x 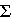 * ->
* ->  recursively as
recursively as
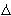 (
(  ,
,  ) =
) = 
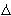 (
(  ,
,  x ) =
x ) = 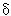 (
( 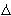 (
(  ,
,  ), x )
), x )
{* |
(
0,
)
F }
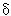 ( 0, x ) = 1.
( 0, x ) = 1.
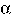
 (i.e. concatenation)
is a bit trickier.
(i.e. concatenation)
is a bit trickier.
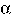 and
and  independently.
independently.
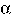 may have many final states.
may have many final states.
 .
.
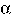 is a* and
is a* and  is aaab*.
is aaab*.
 -transitions.
-transitions.
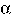 with
with
 -transitions to the initial state in the machine for
-transitions to the initial state in the machine for  .
.
 .
.
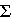 .
.
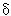 :
:  x (
x (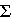 +
+  )
-> 2
)
-> 2 .
.
 called the set of final
states.
called the set of final
states.
 0 of
0 of  called the initial state.
called the initial state.
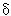 to a function
to a function
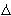 that handles transitions on strings rather than single symbols from
that handles transitions on strings rather than single symbols from 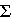 .
.
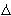 for an FSA, the
for an FSA, the 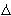 for a NFSA must accept a set
of states and a string as its input:
for a NFSA must accept a set
of states and a string as its input:
: 2
x (
+
)* -> 2
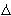 is to take care of the
is to take care of the  productions
by defining the closure of a set of states:
productions
by defining the closure of a set of states:
We define the closure of a set of states, closure(P) to be the smallest set P' such that:
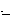 P.
P.
 i
i  P' and
P' and  j
j 
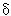 (
(  i,
i,
 ) then
) then  j
j  P'.
P'.
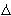 ( P,
( P,  ) = closure( P )
) = closure( P )
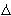 ( P,
( P,  x ) = closure(
x ) = closure( 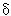 (
( 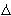 ( P,
( P,  ), x ) ).
), x ) ).
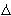 to the initial
state of the machine and the input produce a set of states that includes at least one
of the machine's final states.
to the initial
state of the machine and the input produce a set of states that includes at least one
of the machine's final states.
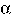 *.
*.
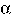 .
.
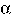 's machine
to this new initial state.
's machine
to this new initial state.
| How Lex Works |