


Go backward to Announcements
Go up to Top
Go forward to Dispersion
Fourier Series (cont.)
- For a periodic signal s(t) of period P = 1/f, Fourier's
showed that
s(t) = (ao)/(2) + 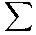 n=1
n=1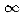 ( an cos( 2
( an cos( 2 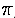 n f t)
+ bn sin(2
n f t)
+ bn sin(2 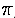 n f t ) )
n f t ) )
where
an = (2)/(P) 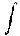 0P s(t) cos( 2
0P s(t) cos( 2 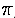 n f t ) dt
n f t ) dt
and
bn = (2)/(P) 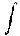 0P s(t) sin( 2
0P s(t) sin( 2 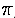 n f t ) dt
n f t ) dt
- Last time, we determined the Fourier coefficients for one
component of the encoding of a digital signal using
frequency modulation. Namely the
d(t) sin( 2
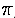 f1 t)
term of the frequency modulated signal described by
f1 t)
term of the frequency modulated signal described by
d(t) sin( 2 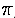 f1 t) + (1 - d(t))sin( 2
f1 t) + (1 - d(t))sin( 2 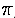 f2 t)
f2 t)
In particular, we concluded that
d(t) sin( 2 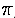 f1 t) =
(sin( 2
f1 t) =
(sin( 2 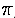 f1 t))/(2) +
f1 t))/(2) +
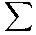 n = 1 and n odd
n = 1 and n odd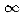 (1)/(
(1)/(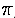 n)( cos( 2
n)( cos( 2 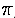 (f1 - n f) t ) +
cos( 2
(f1 - n f) t ) +
cos( 2 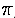 (f1 + n f) t )
(f1 + n f) t )
- This still may not look like a sine wave to you, but
recall that a cosine wave is just a sine wave with a phase
shift. So, we really have expressed s1(t) as the sum
of sine waves with frequencies of the form (f1 ±n f).
- Unfortunately, we again have an infinite set of sine
waves.
- Fortunately, the higher frequency waves have smaller
coefficients AND the frequencies are centered around
the carrier frequency.
- As we expected, the higher the data rate, the wider the spread
of frequencies will be.
- Fortunately, in "real" systems, replacing the square wave
with squares with rounded corners can further reduce the
range of frquencies that are significant.
- If we took the time to account for the other component
of the transmitted signal, (1 - d(t))sin( 2
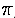 f2 t),
we would obtain a similar series of sine waves with
frequencies of the form (f2 ±n f)
f2 t),
we would obtain a similar series of sine waves with
frequencies of the form (f2 ±n f)
- Thus, the spectrum of the actual signal will consist of
two sequences of sine waves each centered around one or
the frequencies used as a carrier wave.
- If nothing else, these results should let you understand what
is so wonderful about fiber. (The following figures are meant
more to be suggestive of the scale of things than precisely
grounded in reality.)
- The spectrum of visible light falls roughly between
2.5 x 1015 and 5 x 1015Hertz. Thus, the range of
frequencies available for multiplexed signals in this range
is about 2.5 x 1015 hertz.
- When transmitting at one Gigahertz, the span of the
first five terms of a frequency modulated signal
would be about 1010 Hertz.
- The spectrum of visible light could be divided into
roughly 2.5 x 105 channels each capable of
carrying a Gigahertz.
- Now, think about what would happen if instead of using two
frequencies, we used four frequencies to encode 2 bits per
baud.
- If we choose the new frequencies so that they fall between
the two original frequencies, the range of the
spectrum required for the
signal will not increase!
- Thus, in this case, the bandwidth available limits the
baud rate, but not necessarily the bit rate.
- What limits the bit rate is noise on the line (and in
the receiver) which limits how closely together the
frequencies used can fall before we can no longer
distinguish them.
Computer Science 336
Department of Computer Science
Williams College



n=1
( an cos( 2
n f t) + bn sin(2
n f t ) )
0P s(t) cos( 2
n f t ) dt
0P s(t) sin( 2
n f t ) dt
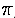 f1 t)
term of the frequency modulated signal described by
f1 t)
term of the frequency modulated signal described by
f1 t) + (1 - d(t))sin( 2
f2 t)
f1 t) = (sin( 2
f1 t))/(2) +
n = 1 and n odd
(1)/(
n)( cos( 2
(f1 - n f) t ) + cos( 2
(f1 + n f) t )
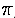 f2 t),
we would obtain a similar series of sine waves with
frequencies of the form (f2 ±n f)
f2 t),
we would obtain a similar series of sine waves with
frequencies of the form (f2 ±n f)