Performance of Sliding Window Protocols

1. In discussing the performance of stop and wait, we ignored the possibility of data errors. If we do the same with sliding window protocols, the behavior of the protocol is determined entirely by the size of the sender's window, W. The size of the receiver's window, B, is irrelevant in this case. In particular, if no packets are damaged, selective repeat and Go Back N perform equally well.

   • If W is large enough, the sender will never pause so the efficiency of the protocol will be 100% (ignoring the fact that transmitting error checking codes and sequence numbers wastes some transmission capacity).

   • Using the same symbols we used when discussing stop and wait's efficiency, if

     W * TR_F > TR_F + TF_A + 2 * P

     then the sender will not pause and the protocol's efficiency will be 1.

   • If

     W * TR_F < TR_F + TF_A + 2 * P

     then the protocol will send W packets , pause waiting for the acknowledgment for the first packet to arrive, then begin sending another batch of W packets (since the ack for each packet sent in the preceding batch should arrive just as the protocol gets ready to send the corresponding packet in the current batch). Accordingly, the efficiency will be:

     ( W * TR_F )/( TR_F + TR_A + 2 * P )

   • This simple analysis is significant for two reasons:

     • In many networks, errors are very rare so the "optimal" efficiency reported by these formulas is close to reality.

     • The fact that there is no difference between selective repeat and Go Back N under these assumptions reveals that the motivations for buffering at the receiver and sender are quite distinct. Buffering at the sender overcomes inefficiencies caused by propagation delay (and other factor that delay acknowledgements such as waiting for data traffic flowing in the opposite direction). Buffering at the receiver is to cope with packet loss.

2. This, of course, implies we should make some attempt to analyze the behavior of these protocols in the presence of errors.

3. A precise analysis of selective repeat or Go Back N is beyond what I would attempt. With a bunch of major simplifying assumptions, however, we can get a rough estimate of its efficiency.

   • Basially, if we make the window size big enough for selective repeat, very few errors will actually lead to situations where the receiver rejects packets because it is still waiting for an undamaged copy of a previous packet.

   • In this case, loss of an acknowledgment becomes unimportant since a later ack informing the sender of the arrival of a packet following the packet whose ack was damaged will take the place of the lost ack at no additional cost. So, our main concern will be the probability, p, of the loss of a packet. We won't explicitly worry about the probability of an ack loss.

   • To calculate the efficiency of selective repeat in the presence of errors, we therefore need to calculate the expected number of transmissions required before a packet is delivered successfully.

   • In general, if the probability that some process will take n steps is p_n, then the expected number of steps is

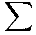
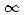     _{n = 1} n p_n

   • In this case, the probability that a packet will take n steps (transmissions) before it is delivered is the probability that errors occur on each of the first n-1 steps times the probability of success on the last step or

     p^n-1 ( 1 - p )

   • So, the expected number of transmissions required for a given packet is:

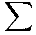
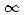     _{n = 1} n p^n-1 (1 - p)

   • If a closed form for this sum doesn't pop into mind immediately, don't panic. The handout on probability I distributed last week mentions a nice trick called the "regenerative method" that lets you determined the expected value without coping with the summation.

     • Let us call the expected number of transmissions required to send a packet successfully E.

     • Observe that at each transmission attempt, there are two possible outcomes. Either everything works (with probability 1-p) and only one step is required; or something doesn't work (with probability p) and you essentially have to start over again.

     • The key point here is the "start over again". Put another way, with probability p, only 1 transmission is required, with probability (1-p) success requires 1 failure followed by a number of transmissions with expected value E.

       So,

       E = 1 ( 1 - p ) + (1 + E) p

     • Solving for E gives

       E = (1)/(1-p)

       (which is the same result you would obtain if you spent a long time working on the summation shown above).

   • So, the number of packets actually delivered in a given amount of time will average the number of packets sent divided by (1)/(1-p). The efficiency of the protocol will be this number divided by the number of packets sent. Therefore, the efficiency will be (1-p).

4. The best case performance of Go Back N is rather different. Assuming the sender's buffer is large enough, lost acks will still be irrelevant. If a packet is actually lost, however, all the packets that follow it will be discarded by the receiver. Once the sender notices the problem (by timing out), it needs to go back (hence the name) to the lost packet and start things over again.

5. The key here is that the behavior of Go Back N can be seen as cycle in which the system works at 100% efficiency for a while as long as no packets are lost. Once a loss occurs, a period of wasted transmissions occurs until the loss is recognized. Then, the sender backs up and starts another period of 100% efficiency.

6. We can estimate the overall efficiency of the protocol by estimating the relative expected lengths of the 100% efficiency periods and the "go back" periods.

7. The expected length of the 100% efficiency period is just the expected number of consecutive error free transmissions times the transmission time, TR_F.

   • If p is the probability that a packet is lost, then 1 - p is the probability it is transmitted successfully. So, the expected number of consecutive successful packet deliveries would be described by the equation

     ED = 0 p + (1 + ED) (1 - p)

   • Solving this equation gives ED = (1/p) - 1

   • For very small values of p, we can therefore approximate ED by 1/p.

8. Using this figure for the length of a run of packets delivered intact, the efficiency of Go Back N can be estimated as

   ((1/p) TR_F)/((1/p) TR_F + TR_F + TR_A + 2 P ) = (TR_F)/(TR_F + p(TR_F + TR_A + 2 P) )

9. Finally, for small values of p, the efficiency of selective repeat, 1-p, is very closely approximated by 1/(1+p). Multiplying this formula top and bottom by TR_F yields a formula for selective repeat's efficiency that is easily compared to the formula for Go Back N:

   (TR_F)/(TR_F + p(TR_F) )