



Predicting What Students Know
An Introduction to Bayesian Knowledge Tracing
Bayesian Knowledge Tracing, or BKT, is an artificial intelligence
algorithm that lets us infer a student's current knowledge state to
predict if they have learned a skill.
There are four parameters involved in BKT (each with a value between 0 and 1, inclusive):
-
P(known):
the probability that the student already knew a skill.
-
P(will learn):
the probability that the student will learn a skill on the next practice opportunity.
-
P(slip):
the probability that the student will answer incorrectly despite knowing a skill.
-
P(guess):
the probability that the student will answer correctly despite not knowing a skill.
Every time the student answers a question, our BKT algorithm calculates
P(learned), the probability that the student has learned the skill
they are working on, using the values of these parameters.
The formula for P(learned) depends on whether their response was correct.
First, we compute the conditional probability that the student
learned the skill previously (at time n-1), based on whether
they answered the current question (at time n) correctly or incorrectly.
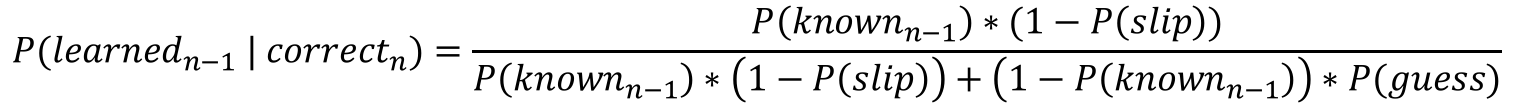
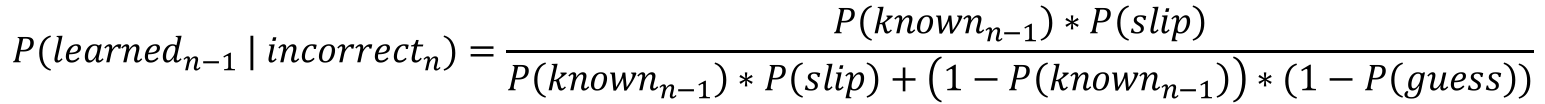
Then, we use the result of our first calculation to compute the
conditional probability that the student has learned the skill now
(at time n).
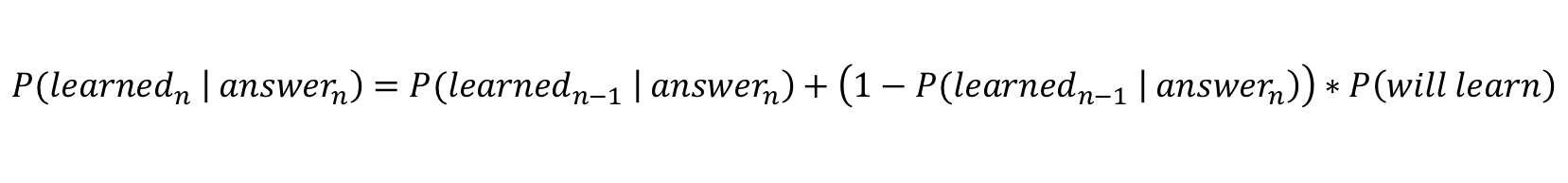
For the next question, we use P(learned) as the new value of P(known).
Once P(known) ≥ 0.95, we say that the student has achieved
m
a
s
t
e
r
y.
Now that you’ve had a chance to learn about the four parameters,
here’s a tool that can help you visualize the relationships between them
and explore how each one influences the probability calculations underlying BKT.
We'll be modeling the system with a hot air balloon, using its height as a
measure of mastery.
First, we compute the conditional probability that the student learned the skill previously (at time n-1), based on whether they answered the current question (at time n) correctly or incorrectly.
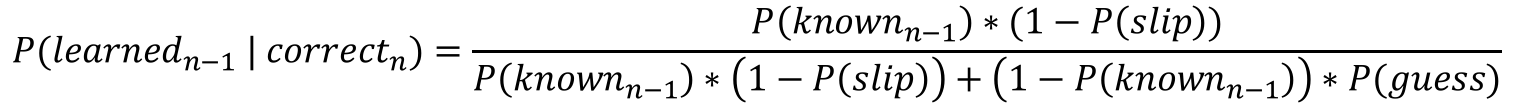
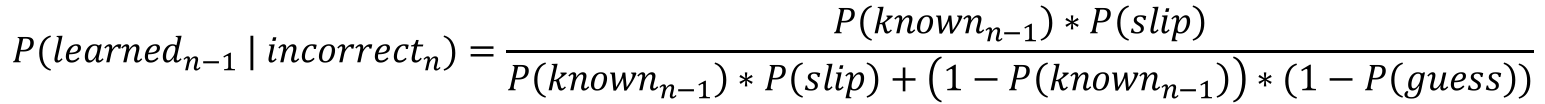
Then, we use the result of our first calculation to compute the conditional probability that the student has learned the skill now (at time n).
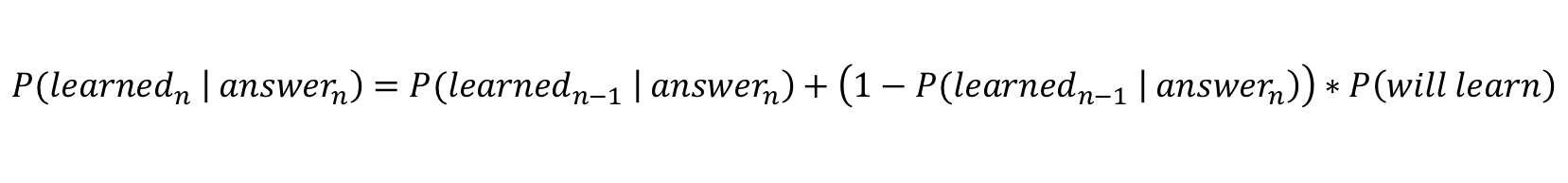
Let's begin!
