Randomized Controlled Experiments#

from datascience import *
from cs104 import *
import numpy as np
%matplotlib inline

1. Warm-up Permutation Test#

survey = Table().read_table('data/prelab01-survey-fall2023.csv')
survey = survey.where('Left or Right Handed', are.not_equal_to('Ambidextrous'))
survey
Year at Williams Favorite Icecream Flavor Favorite Planet Height (in inches) Distance Home (in miles) Birth Month Left or Right Handed
2 Strawberry Venus 60 175 October Right
1 Coffee Venus 63 6831 March Right
2 Chocolate Earth 74 2600 July Right
1 Chocolate Saturn 64 141 July Right
1 Chocolate Earth 66 132.8 October Right
1 I don't like icecream! Earth 73 2023 October Right
2 Vanilla Saturn 66 1685.7 June Right
2 Chocolate Pluto 69 167.5 April Right
2 Chocolate Jupiter 62 170 December Right
4 Vanilla Earth 71 7233 January Right

... (47 rows omitted)

survey.group('Left or Right Handed', np.mean)
Left or Right Handed Year at Williams mean Favorite Icecream Flavor mean Favorite Planet mean Height (in inches) mean Distance Home (in miles) mean Birth Month mean
Left 2.8 69.6 1419.4
Right 2.30769 68.6362 1295.68 
observed = abs_difference_of_means(survey, 'Left or Right Handed', 'Height (in inches)')
observed

0.9638461538461485

Is the height difference significant?

results = simulate_permutation_statistic(survey, 'Left or Right Handed', 'Height (in inches)', 1000)

plot = Table().with_columns('abs_difference_of_means', results).hist(left_end=observed)
plot.set_title('Null hypothesis empirical distibution')
plot.dot(observed)
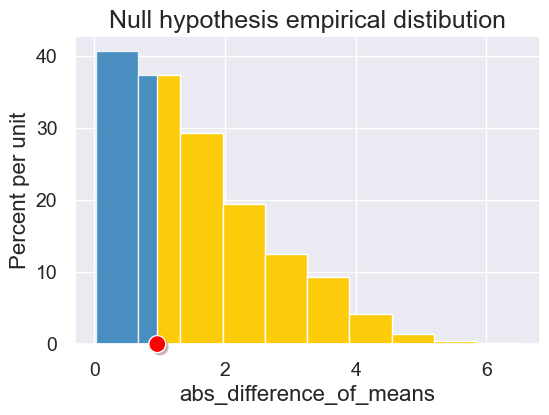
../_images/23-randomized-controlled-experiments_8_0.png 
p_value = empirical_pvalue(results, observed)
p_value

0.653

2. Randomized Controlled Experiment with BTA#

rct = Table.read_table('data/bta.csv')
rct.sample(10)
Group Result
Control 0
Treatment 1
Control 0
Treatment 1
Treatment 1
Treatment 0
Treatment 1
Control 0
Control 0
Treatment 1 
rct.group('Group')
Group count
Control 16
Treatment 15 
rct.pivot('Result', 'Group')
Group 0.0 1.0
Control 14 2
Treatment 6 9 
rct.group('Group', np.mean)
Group Result mean
Control 0.125
Treatment 0.6

Permutation Testing#

observed_statistic = abs_difference_of_means(rct, 'Group', 'Result')
observed_statistic

0.475

type(observed_statistic)

float

results = simulate_permutation_statistic(rct, 'Group', 'Result', 2000)

plot = Table().with_columns('Abs Difference in Relief Proportions', results).hist(bins=np.arange(0,0.9,1/16))
plot.set_title('Null hypothesis empirical distibution')
plot.dot(observed_statistic)
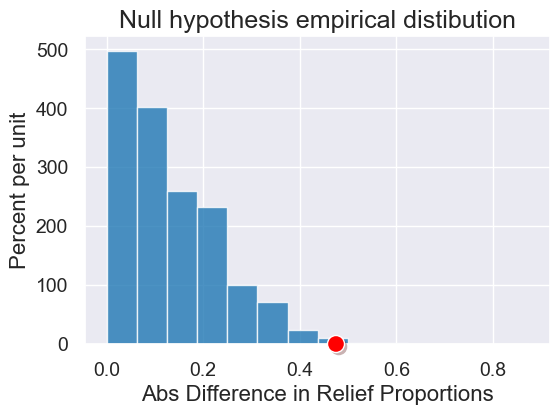
../_images/23-randomized-controlled-experiments_19_0.png 
p_value = empirical_pvalue(results, observed_statistic)
p_value

0.009

3. Sample Size, Effect Size, and P-values#

What’s the relationship between effect size, sample size, and p-value?

What we had before.

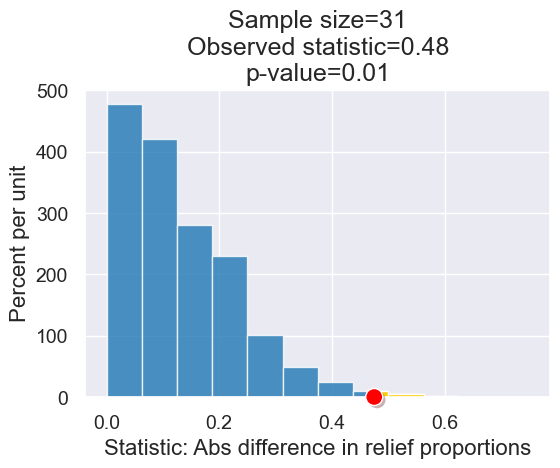
../_images/23-randomized-controlled-experiments_25_0.png

What if the effect size was slightly smaller? What if the sample size was bigger?

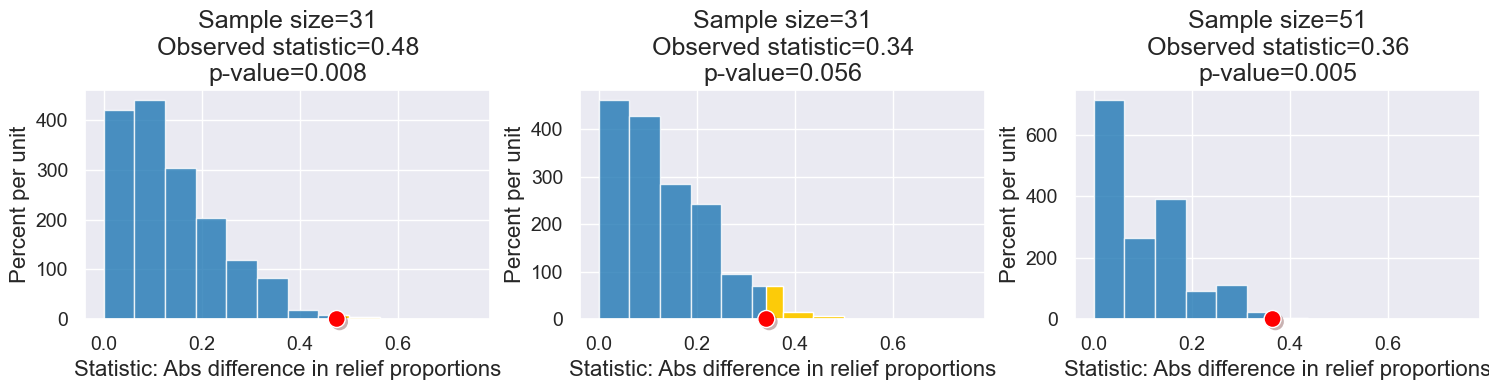
../_images/23-randomized-controlled-experiments_27_0.png

Let’s look at all these relationships at once!

The following cell contains an interactive visualization. You won’t see the visualization on this web page, but you can view and interact with it if you run this notebook on our server here.

interact(back_pain_exploration, 
         observed_sample_size=Slider(10, 200, 1), 
         treatment_prop_effective=Slider(0.05, 0.95, 0.01),
         control_prop_effective=Slider(0.05, 0.95, 0.01))

Here’s an animation showing the effects above.