Contents

Boostrapping

from datascience import *
%matplotlib inline
import matplotlib.pyplot as plots
plots.style.use('fivethirtyeight')
import numpy as np
import warnings
warnings.simplefilter(action='ignore', category=np.VisibleDeprecationWarning)
warnings.simplefilter(action='ignore', category=UserWarning)

from ipywidgets import interact, interactive, fixed, interact_manual
import ipywidgets as widgets

1. Median and percentiles

# A tiny set of salaries

# These are sorted, but they don't need to be to use percentile.
tiny_salaries = make_array(1317,  3909,  6015,  7467, 18632, 20828, 20950)
tiny_salaries

array([ 1317,  3909,  6015,  7467, 18632, 20828, 20950])

percentile(50, tiny_salaries)

7467

percentile(75, tiny_salaries)

20828

2. Boostrapping

# Load the 200-sample of Boston city police officers.
boston_sample = Table().read_table('data/boston-earnings-small.csv')
boston_sample.show(5)
TITLE REGULAR TOTAL_GROSS
Police Officer 89969 180643
Police Officer 83065 148513
Police Officer 91784 150195
Police Officer 25923 90898
Police Officer 35882 36068

... (195 rows omitted)

boston_sample.num_rows

200

boston_sample.hist('REGULAR')
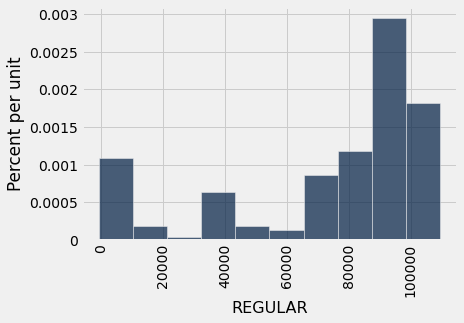
../_images/24-bootstrapping_10_0.png 
sample_median = percentile(50, boston_sample.column('REGULAR'))
sample_median

89969

def bootstrap(observed_sample, num_trials): 

    bootstrap_statistics = make_array()
    
    for i in np.arange(0, num_trials): 
        #Key: in bootstrapping we must always sample with replacement 
        simulated_resample = boston_sample.sample()
        
        resample_statistic = percentile(50, simulated_resample.column('REGULAR')) #get the median for that one resample 
        bootstrap_statistics = np.append(bootstrap_statistics, resample_statistic)
    
    return bootstrap_statistics

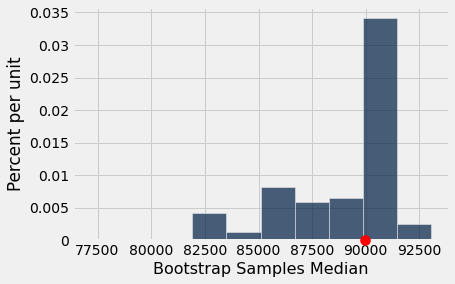
bootstrap_statistics = bootstrap(boston_sample, 10000)

# Put in Table and analyze results 
results = Table().with_column('Bootstrap Samples Median', bootstrap_statistics)
results.hist()
#Plot the median of our original sample in red
plots.scatter(sample_median, 0, color='red', s=100, zorder=10, clip_on=False);
../_images/24-bootstrapping_14_0.png

3. “Oracle” Evaluation

Oracle: pretend we are an all-knowing being and can look at the true population (which our journalist does not have access to)

We can check agaist the population for the pedagogical purposes of understanding the bootstrap. However, in the real world we would mostly likely only have the sample. And if we did have the population, we wouldn’t need to bootstrap.

population = Table().read_table('data/boston-earnings.csv')
population = population.select('TITLE', 'REGULAR', 'TOTAL_GROSS')
population = population.where('TITLE', are.equal_to('Police Officer'))
population.show(5)
TITLE REGULAR TOTAL_GROSS
Police Officer 0 1264844
Police Officer 0 1252991
Police Officer 100963 399826
Police Officer 99102 306588
Police Officer 91784 304577

... (1316 rows omitted)

population.hist('REGULAR')
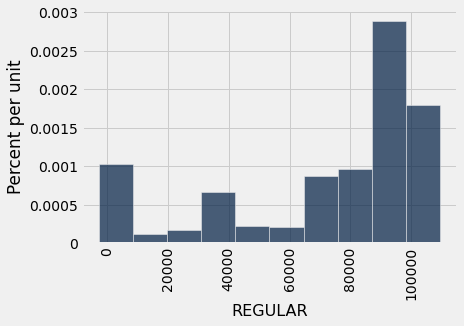
../_images/24-bootstrapping_17_0.png 
#median of the population 
population_salaries = population.column('REGULAR')
true_parameter = percentile(50, population_salaries)
true_parameter

89717

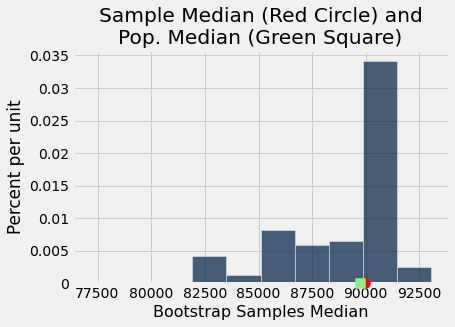
# Compare the true parameter to our bootstrap estimate
results.hist()
#Plot the median of our original sample in red
plots.scatter(sample_median, 0, color='red', s=100, zorder=10, clip_on=False)
#Plot the true population parameter in green 
plots.scatter(true_parameter, 0, color='lightgreen', marker='s', s=100, zorder=10, clip_on=False)
plots.title('Sample Median (Red Circle) and\nPop. Median (Green Square)');
../_images/24-bootstrapping_19_0.png

Sensitivity to Sample Size and Number of Samples

Here’s a way to visualize how the bootstrap distribution converges to the same distribution as the one for samples from the population.

# random_seed lets us change the random numbers used to pick samples 
# Basically, changing the seed let's us generated different samples.
# random_seed 0 uses boston_sample from above.  All others create new initial sample
def visualize_bootstrap(random_seed, sample_size, num_samples):
    np.random.seed(random_seed)
    if random_seed == 0:
        first_sample = boston_sample
    else:
        first_sample = population.sample(sample_size, with_replacement=False)
    medians = Table(["Type", "Median"])
    sample_medians = make_array()
    
    for i in np.arange(num_samples):
        sample = population.sample(sample_size)
        sample_median = percentile(50, sample.column('REGULAR'))
        medians.append([ "Realworld", sample_median ])

    for i in np.arange(num_samples):
        bootstrap_sample = first_sample.sample()
        boostrap_median = percentile(50, bootstrap_sample.column('REGULAR'))
        medians.append([ "Bootstrap", boostrap_median ])

    median_bins=np.arange(75000, 95000, 1000)
    medians.hist(group="Type", bins=median_bins)

    # Plotting parameters; you can ignore this code
    plots.scatter(true_parameter, 0.000005, color='lightgreen', marker="s", s=100, zorder=12, clip_on=False)
    plots.scatter(np.median(first_sample.column('REGULAR')), 0.000005, color='red', s=100, zorder=12, clip_on=False)
    plots.title('Bootstrap/Real World Medians\nSample Median (Red Dot); Pop Median (Green Square)\nsample size = ' + str(sample_size) + '; num samples = ' + str(num_samples));        
    
_ = widgets.interact(visualize_bootstrap, 
                     random_seed=(0,100,1),
                     sample_size=make_array(25, 50,100,200,500, 1000,2000), 
                     num_samples=make_array(20,200,2000))