Contents

Probability and Sampling

from datascience import *
import numpy as np

%matplotlib inline
import matplotlib.pyplot as plots
plots.style.use('fivethirtyeight')

from ipywidgets import interact, interactive, fixed, interact_manual
import ipywidgets as widgets

1. Distributions

Probability Distribution

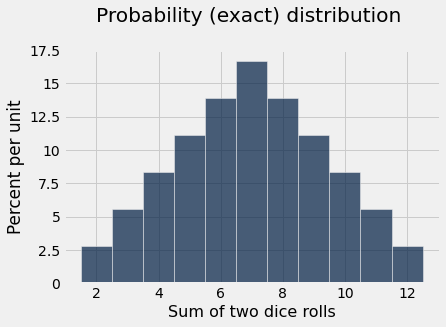
We have used probability rules to analytically write down the expected number of each possible value in order to create a probability distribution.

# Sums of all possible combinations of two dice rolls. 
# (The first few entries illustrate how we constructed these combinations.)
outcomes = make_array(1+1,1+2,2+1,1+3,2+2,3+1,5,5,5,5,6,6,6,6,6,
                      7,7,7,7,7,7,8,8,8,8,8,9,9,9,9,10,10,10,11,11,12)
outcome_bins = np.arange(1.5, 13.5, 1)
Table().with_columns('Sum of two dice rolls', outcomes).hist(bins=outcome_bins)
plots.title('Probability (exact) distribution \n   ')
plots.ylim(0,0.175);
../_images/16-sampling_5_0.png

Empirical Distribution

dice = np.arange(1,7)
dice

array([1, 2, 3, 4, 5, 6])

#roll the dice twice and add the values 
two_dice = np.random.choice(dice, 2)
print('two dice=', two_dice)
print('sum=', sum(two_dice))

two dice= [1 4]
sum= 5

Use our standard loop idiom to build an array of the sums of two dice.

num_trials = 2000 
all_outcomes = make_array()
for i in np.arange(0,num_trials):
    outcome = sum(np.random.choice(dice, 2))
    all_outcomes = np.append(all_outcomes, outcome) 
simulated_results = Table().with_column('Sum of two dice rolls', all_outcomes)
simulated_results
Sum of two dice rolls
9
6
10
7
5
9
8
5
4
3

... (1990 rows omitted)

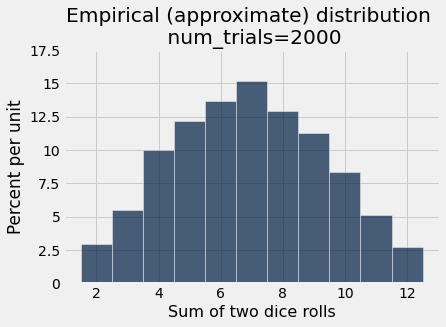
simulated_results.hist(bins=outcome_bins)
plots.title('Empirical (approximate) distribution \n num_trials='+str(num_trials));
plots.ylim(0,0.175);
../_images/16-sampling_11_0.png

Law of Averages

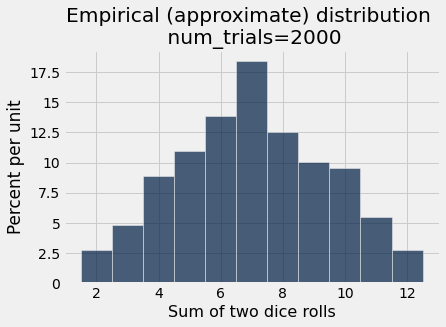
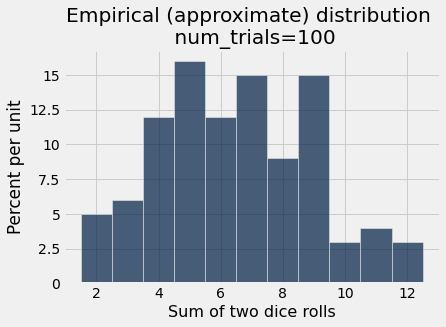
In our simulation, we have one parameter that we have the ability to control num_trials. Does this parameter matter?

To find out, we can write a function that takes as input the num_trials parameter.

def simulate_and_plot_summing_two_dice(num_trials):
    """
    Simulates rollowing two dice and repeats num_trials times, and 
    Plots the empirical distribution
    """
    all_outcomes = make_array()
    for i in np.arange(0,num_trials):
        outcome = sum(np.random.choice(dice, 2))
        all_outcomes = np.append(all_outcomes, outcome) 
    simulated_results = Table().with_column('Sum of two dice rolls', all_outcomes)
    simulated_results.hist(bins=outcome_bins)
    plots.title('Empirical (approximate) distribution \n num_trials='+str(num_trials));

simulate_and_plot_summing_two_dice(2000)
../_images/16-sampling_15_0.png 
simulate_and_plot_summing_two_dice(100)
../_images/16-sampling_16_0.png 
simulate_and_plot_summing_two_dice(500)
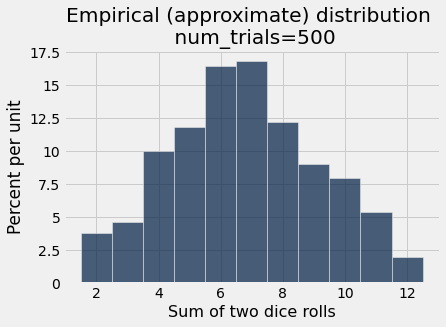
../_images/16-sampling_17_0.png 
simulate_and_plot_summing_two_dice(10000)
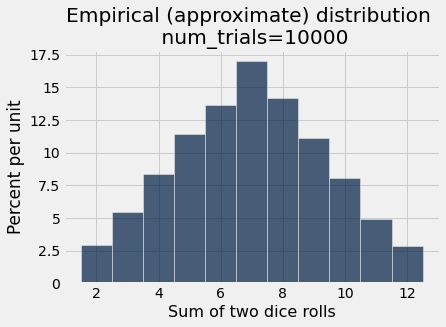
../_images/16-sampling_18_0.png

If you run this notebook yourself, you can use the following interactive plot to see how the number of trials impacts the result.

_ = widgets.interact(simulate_and_plot_summing_two_dice, num_trials = (1,20000))

2. Random Sampling: Florida Votes in 2016

Load data for voting in Florida in 2016. These give us the true parameters if we were able to poll every person who would turn out to vote:

  • Proportion voting for (Trump, Clinton, Johnson, other) = (0.49, 0.478, 0.022, 0.01)

  • Raw counts:

    • Trump: 4,617,886

    • Clinton: 4,504,975

    • Johnson: 207,043

    • Other: 90,135

Data is based on the actual votes case in the election.

votes = Table().read_table('data/florida_2016.csv')
# the csv file uses 0,1,2,3 for the four choices, so we must convert them to candidate names
votes = votes.with_column('Vote', votes.apply(make_array("Trump", "Clinton", "Johnson", "Other").item, "Vote"))

votes.show(5)
Vote
Clinton
Trump
Trump
Clinton
Trump

... (9420034 rows omitted)

# total number of votes cast in election.
votes.num_rows

9420039

We can pick a “convenience sample”: the first 10 voters who show up in line.

votes.take(np.arange(10))
Vote
Clinton
Trump
Trump
Clinton
Trump
Johnson
Clinton
Clinton
Clinton
Trump

Since we actually know the votes for the full population, we can compute the true parameter.

sum(votes.column('Vote') == 'Trump') / votes.num_rows

0.49021941416590736

But suppose this is before the election and we actually can’t ask every person in the state how they will vote…

In that case, we can imagine we are a pollster, and sample 50 people.

We can use .sample(n) to randomly sample n rows from a table.

sample = votes.sample(50)
sample
Vote
Clinton
Trump
Clinton
Trump
Clinton
Clinton
Trump
Clinton
Trump
Clinton

... (40 rows omitted)

sum(sample.column('Vote') == 'Trump') / sample.num_rows

0.52

Sampling and computing the proportion of Trump votes in one function

def sample_proportion_vote_trump(sample_size): 
    """
    Randomly samples sample_size number of rows from the votes table
    Returns the proportion that voted for Trump 
    """
    sample =  votes.sample(sample_size)
    proportion_trump = sum(sample.column('Vote') == 'Trump') / sample.num_rows
    return proportion_trump

sample_proportion_vote_trump(100)

0.56

sample_proportion_vote_trump(1000)

0.471

Let’s use our simulation algorithm to create an empirical distribution.

Suppose there are 1,000 polling companies and each uses a sample of 100 people.

num_trials = 1000
sample_size = 100

all_outcomes = make_array()
for i in np.arange(0,num_trials):
    outcome = sample_proportion_vote_trump(sample_size)
    all_outcomes = np.append(all_outcomes, outcome) 

simulated_results = Table().with_column('Proportion voting for Trump', all_outcomes)
simulated_results.hist()

title = 'Empirical (approximate) distribution \n num_trials='+str(num_trials)+ '\n sample_size='+str(sample_size)
plots.title(title);
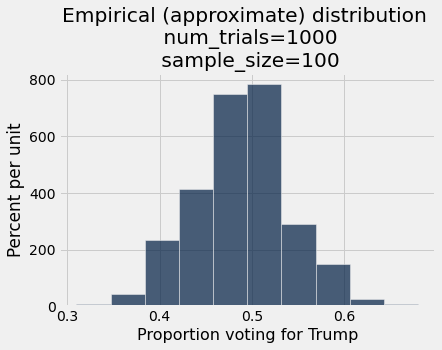
../_images/16-sampling_39_0.png

Let’s make a function with our two free parameters, num_trials and sample_size.

def simulate_and_plot_trump_pollster(num_trials, sample_size): 
    all_outcomes = make_array()
    for i in np.arange(0,num_trials):
        outcome = sample_proportion_vote_trump(sample_size)
        all_outcomes = np.append(all_outcomes, outcome) 
    simulated_results = Table().with_column('Proportion voting for Trump', all_outcomes)
    simulated_results.hist()
    title = 'Empirical (approximate) distribution \n num_trials='+str(num_trials)+ '\n sample_size='+str(sample_size)
    plots.title(title);

simulate_and_plot_trump_pollster(1000, 500)
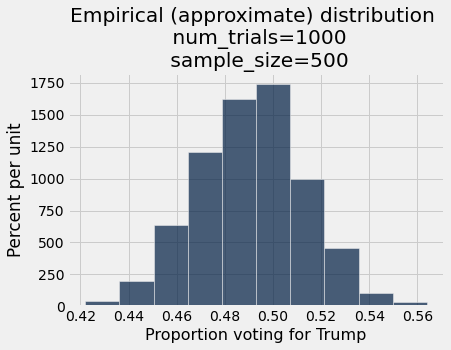
../_images/16-sampling_42_0.png 
simulate_and_plot_trump_pollster(5000, 1000)
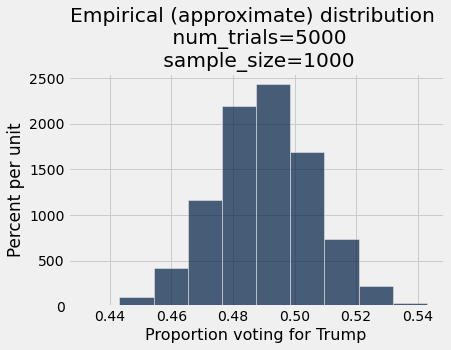
../_images/16-sampling_43_0.png

If you run this notebook yourself, you can use the following interactive plot to see how the number of trials and sample size impact the result.

_ = widgets.interact(simulate_and_plot_trump_pollster, 
                     num_trials = make_array(1,10,100,1000,5000), 
                     sample_size=make_array(1,10,100,1000,5000))

Big picture questions sampling:

  • Why wouldn’t we always just take really big of samples since they converge to the true distribution?

Big picture questions simulations:

  • What are we abstracting away when we’re writing code? What are we re-using over and over?