Simulation¶
from datascience import *
import numpy as np
%matplotlib inline
import matplotlib.pyplot as plots
plots.style.use('fivethirtyeight')
import warnings
warnings.simplefilter(action='ignore', category=np.VisibleDeprecationWarning)
1. Coins¶

If you flip a fair coin 100 times, how often can you expect to get between 40 and 60 heads?
Generic simulation algorithm:
Repeat N times:
Simulate one trial
Record the outcome
Make table of all the outcomes and analyze results
Simulating One Trial¶
coin = make_array('heads', 'tails')
np.random.choice(coin)
'tails'
tosses = np.random.choice(coin, 100)
tosses
array(['tails', 'heads', 'heads', 'heads', 'tails', 'tails', 'heads',
'heads', 'heads', 'tails', 'heads', 'tails', 'tails', 'heads',
'heads', 'tails', 'tails', 'heads', 'tails', 'heads', 'tails',
'tails', 'heads', 'heads', 'heads', 'heads', 'tails', 'heads',
'tails', 'heads', 'tails', 'heads', 'tails', 'tails', 'tails',
'tails', 'tails', 'heads', 'tails', 'heads', 'tails', 'heads',
'tails', 'tails', 'heads', 'heads', 'tails', 'tails', 'tails',
'tails', 'tails', 'tails', 'tails', 'heads', 'tails', 'heads',
'tails', 'heads', 'heads', 'tails', 'tails', 'heads', 'heads',
'heads', 'tails', 'tails', 'heads', 'tails', 'heads', 'heads',
'tails', 'heads', 'tails', 'tails', 'tails', 'heads', 'heads',
'heads', 'tails', 'tails', 'tails', 'heads', 'heads', 'heads',
'tails', 'tails', 'heads', 'tails', 'heads', 'tails', 'tails',
'tails', 'heads', 'heads', 'tails', 'heads', 'heads', 'tails',
'tails', 'heads'], dtype='<U5')
sum(tosses == 'heads')
47
All in one cell: run it a bunch!
#In our case, the outcome is the number of heads that appear in 100 tosses
outcome = sum(np.random.choice(coin, 100) == 'heads')
outcome
56
Running Many Trials: For Loops¶
num_trials = 10
for i in np.arange(0,num_trials):
outcome = sum(np.random.choice(coin, 100) == 'heads')
print(outcome)
46
47
52
44
52
46
49
51
46
49
Recording the outcome: appending to an array of outcomes¶
We need some way to record the outcome for each trial (each iteration of our for loop).
all_outcomes = make_array()
One simulation: run it a bunch!
outcome = sum(np.random.choice(coin, 100) == 'heads')
all_outcomes = np.append(all_outcomes, outcome)
all_outcomes
array([46.])
All in one cell:
num_trials = 10000
all_outcomes = make_array()
for i in np.arange(0,num_trials):
outcome = sum(np.random.choice(coin, 100) == 'heads')
all_outcomes = np.append(all_outcomes, outcome)
all_outcomes
array([51., 37., 47., ..., 54., 43., 53.])
Now let’s create a table so we can easily analyze the results.
simulated_results = Table().with_column('Heads in 100 flips', all_outcomes)
simulated_results.hist(bins=np.arange(30, 70, 1))
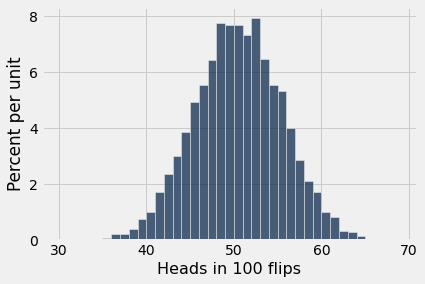
target_range = simulated_results.group("Heads in 100 flips").where("Heads in 100 flips", are.between(40,60))
target_range
| Heads in 100 flips | count |
|---|---|
| 40 | 101 |
| 41 | 174 |
| 42 | 238 |
| 43 | 303 |
| 44 | 387 |
| 45 | 495 |
| 46 | 555 |
| 47 | 643 |
| 48 | 776 |
| 49 | 770 |
... (10 rows omitted)
sum(target_range.column("count")) / simulated_results.num_rows
0.9546
2. The Monty Hall Problem¶
Three doors hide two goats and a car.
You pick one of three doors.
A different door is opened to reveal a goat.
You must decide which door has the car. You can stick with your original choice, or you can switch to the other unopened door.
Which choice (staying or switching) gives you the greatest chance of winning the car?
hidden_behind_doors = make_array('goat', 'goat', 'car')
hidden_behind_doors
array(['goat', 'goat', 'car'], dtype='<U4')
Define functions that give you the result of one trial. Both pick the initial door at random, and then determine which door the player ultimately selects based on our two strategies.
def monty_hall_game_staying_strategy():
"""
Return what player wins if they stick with their original choice
"""
return np.random.choice(hidden_behind_doors)
def monty_hall_game_switching_strategy():
"""
Return what player wins if they switch with their original choice
"""
contestant_guess = np.random.choice(hidden_behind_doors)
if contestant_guess == 'car':
# Revealed door is one goat ...
# ... and the remaining door is the second goat.
return 'goat'
else:
# Releaved door is the second goat ...
# ... and the remaining door is the car.
return 'car'
monty_hall_game_staying_strategy()
'goat'
monty_hall_game_switching_strategy()
'car'
Which strategy wins the car with higher probability?
num_trials = 10000
staying = make_array()
for i in np.arange(num_trials):
staying = np.append(staying, monty_hall_game_staying_strategy())
print ("Win car if staying:", sum(staying == 'car') / num_trials)
switching = make_array()
for i in np.arange(num_trials):
switching = np.append(switching, monty_hall_game_switching_strategy())
print ("Win car if switching:", sum(switching == 'car') / num_trials)
Win car if staying: 0.3337
Win car if switching: 0.6638
Chance of At Least One Success in Repeated Independent Trials¶
Chance of no fours in 5 rolls of a die?
prob_no_fours_in_five_rolls = (5/6) ** 5
prob_no_fours_in_five_rolls
0.401877572016461
Chance of at least one 4 in 5 rolls of a die?
1 - prob_no_fours_in_five_rolls
0.598122427983539
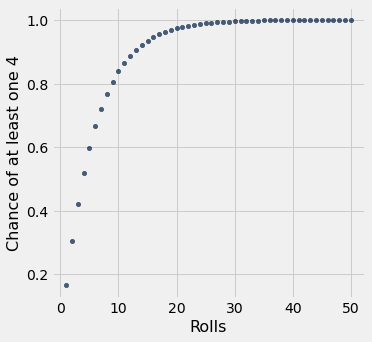
Chance of at least one four in n rolls of a die?
rolls = np.arange(1, 51, 1)
results = Table().with_columns(
'Rolls', rolls,
'Chance of at least one 4', 1 - (5/6)**rolls
)
results
| Rolls | Chance of at least one 4 |
|---|---|
| 1 | 0.166667 |
| 2 | 0.305556 |
| 3 | 0.421296 |
| 4 | 0.517747 |
| 5 | 0.598122 |
| 6 | 0.665102 |
| 7 | 0.720918 |
| 8 | 0.767432 |
| 9 | 0.806193 |
| 10 | 0.838494 |
... (40 rows omitted)
results.scatter('Rolls')