| LR Parsing |
By way of review:
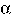

 such that
such that
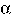 ,
,  ,
, 
 (Vn U Vt)* ,
(Vn U Vt)* ,
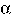


 Vn, U
Vn, U


 P and
P and
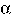 U
U  is a sentential form of G
is a sentential form of G
 is a simple phrase of the
sentential form w.
is a simple phrase of the
sentential form w.
< E >
 < E > + < T > | < T >
< E > + < T > | < T >
< T >
 a | ( < E > )
a | ( < E > )
| < E > |
 < E > + < T >
< E > + < T > | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 < E > + a
< E > + a | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 < E > + < T > + a
< E > + < T > + a | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 < E > + ( < E > ) + a
< E > + ( < E > ) + a | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 < E > + ( < E > + < T > ) + a
< E > + ( < E > + < T > ) + a | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 < E > + ( < E > + a ) + a
< E > + ( < E > + a ) + a | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| . . . | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Any prefix of any sentential from in such a derivation that does not extend past the handle should be considered a viable prefix.

< E >
< E > +
< E > + < T >

< E >
< E > +
< E > + a
 < E > + ( < E > + < T > ) + a
< E > + ( < E > + < T > ) + a
< E > + (
< E > + ( < E >
< E > + ( < E > +
< E > + ( < E > + < T >

 (Vn U Vt)* is a viable prefix of G
if there exists a rightmost derivation
(Vn U Vt)* is a viable prefix of G
if there exists a rightmost derivation
Ssuch that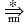
N
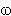
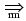
1
2
 =
= 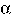
 1.
1.
As long as the prefix of a sentential form of a shift-reduce parser is a viable prefix for the associated grammar, things are OK (i.e. we have not yet read past the handle and there is at least some possible remaining input that could form a valid sentential form and some hope of finding a rightmost parse of this sentential form).
We will demonstrate this by explaining how to build a finite state machine that recognizes the set of viable prefixes of a context free grammar.
< S >
 a < B > | b < A > | b c
a < B > | b < A > | b c
< A >
 b
b
< B >
 b | c
b | c
< S >
 b < A >
b < A >
< A >
 b
b
< S >
 b c
b c
[ Nis an LR(0) item or LR(0) configuration for G if N
1 .
2 ]

 1
1  2 is a production in G.
2 is a production in G.
For example, the configuration set:
< S >
 b . < A >
b . < A >
< S >
 b . c
b . c
< A >
 . b
. b

 1 .
1 .  2 ]
,
is valid for
2 ]
,
is valid for 
 ( Vn U Vt )* if there is a
rightmost derivation
( Vn U Vt )* if there is a
rightmost derivation
Ssuch that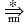
N
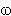
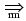
1
2
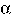
 1 =
1 =  .
.
 then
then  must be a viable prefix.
must be a viable prefix.
 is a viable prefix, then there must be
some LR(0) item that is valid for
is a viable prefix, then there must be
some LR(0) item that is valid for  .
.
< S >
 a < B > | b < A > | b c
a < B > | b < A > | b c
< A >
 b
b
< B >
 b | c
b | c
[ < S >
 . a < B > ]
. a < B > ] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[ < S >
 . b < A > ]
. b < A > ] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[ < S >
 . b c ]
. b c ]
|
[ < S >
 a . < B > ]
a . < B > ]
[ < B >
 . b ]
. b ]
[ < B >
 . c ]
. c ]
| LR Parsing |