Reasoning About Code, Part 2
Table Of Contents
Based on notes by Krysta Yousoufian, Hal Perkins, Michael Ernst, David Notkin, and Dan Grossman
Reasoning about loops
When you hear “loop,” you might think immediately of a for loop, but we’re going to focus on the more fundamental while loop:
while (B) {
S;
}for loops can, of course, can be rewritten using while. The loop
for ( init ; test ; step ) {
S;
}is equivalent to
init;
while (test) {
S;
step;
}so we lose no generality by restricting our attention to while. (There is one difference we won’t emphasize here: The meaning of continue is different for the two kinds of loops: For the for-loop, continue will execute step before the next iteration.)
When reasoning about a chunk of code involving a loop, there’s often an initialization step between the precondition and the start of the loop. The complete code looks more like:
{P}
[initialization steps]
while (B) {
S;
}
{Q}Loops are trickier to reason about than assignment and if/else statements because you don’t know how many times the loop body will execute. We have to show that our code is correct if the loop iterates 0 times, 1 times, 2 times, 3 times, 4 times, …. More generally, we need to prove that when the loop terminates, {Q} is satisfied regardless of how many times the loop ran. (We also need to prove that the loop will terminate, but we won’t worry too much about that for now.) To do this, we introduce the notion of a loop invariant.
A loop invariant, usually written {I}, is a precondition and postcondition for the loop body. {I} must be true at the beginning and end of each iteration of the loop body, though it does not need to hold at every point in the middle of the loop. To show that a given loop invariant is valid, we show: 1. that it holds immediately before entering the loop and 2. that if it holds at the beginning of the loop, it also holds at the end.
- implies that
{I}holds at the beginning of the first iteration. (We assume that evaluating B does not change any variables). By induction, we can then conclude that{I}holds at the beginning and end of every iteration. (Why?) We can also use the fact that{B}is true at the beginning of every iteration or the loop would have terminated.
Since {I} holds true at the end of any iteration, including the final iteration, it must also hold true immediately after the loop exits. We also know {B} is false when the loop terminates or the loop wouldn’t have stopped. So to prove that {Q} holds after the loop, we just need to show that {IΛ!B}=>{Q}. (You may have noticed an edge case: what if the loop terminates immediately so the loop body is never executed? Since {I} held before the non-executed loop, it will still hold afterward.)
In summary, to prove that the postcondition is satisfied and our code is correct, we need to show:
- That
{I}holds immediately before the loop, i.e., immediately after the initialization steps. - That
{I}holds at the end of the loop body, given that{I Λ B}hold at the beginning of the loop body. - That
{I Λ !B}=>{Q}
Let’s add these assertions to our generalized loop:
{P}
[initialization steps]
{I}
while (B) {
{I Λ B}
S;
{I}
}
{I Λ !B} => {Q}Sound easy? The clever part is finding the loop invariant that makes these three conditions true. We often can get inspiration by looking at the postcondition {Q}. Very often a suitable invariant {I} is a weaker version of {Q} that captures how the loop has achieved part of the desired result, but not all.
As we will see in the examples below, this reasoning process should be performed as you are writing the code , shaping what you write. It guides your thought process to help you write clean and correct code on the first try.
When writing loops, you may be tempted to write your code sequentially, starting with {P} and working your way to {Q} one line at a time. It is usually more effective to work from the inside out in roughly the following order:
- Choose a loop invariant and write the loop body (in either order – this is the inventive step).
- Choose B so that {I Λ !B} => {Q}.
- Add initialization steps to get from {P} to {I}.
This order isn’t a hard-and-fast rule, but it’s a good place to start.
Example 1: Sum
Write a loop to set sum = 1 + 2 + … + n and prove that it is correct.
From the instructions, we have our postcondition: {sum = 1 + 2 + ... + n}.
Let’s start with the loop body. We’ll need a counter k. At each iteration, we’ll add k to sum and increment k. So far, our code looks something like this:
{pre: ____________}
[Initialization]
{inv: ____________}
while (B:__________) {
{inv: ____________}
sum = sum + k;
k = k+1;
{inv: ____________}
}
{post: sum = 1 + 2 + ... + n}(To aid readability, we use {pre: ...} to denote a precondition, {post: ...} to denote a postcondition, and {inv: ...} to denote a loop invariant.)
What should our loop invariant be? In the loop body, we add k to sum and increment k. This suggests that sum should be 1 + 2 + ... + k-1 going into the loop body. Let’s call this assertion {I}. If {I} holds at the beginning of the loop, is it guaranteed to hold at the end of the loop? We can find out by writing it as the postcondition for the loop body and reasoning backwards to find the weakest precondition:
{sum = 1 + 2 + ... + k-1}
sum = sum + k;
{sum = 1 + 2 + ... + k}
k = k+1;
{sum = 1 + 2 + ... + k-1}Yes, if {I} holds at the beginning of the loop, the fact that we add k to sum and increment k will ensure that {I} also holds at the end of the loop. We will use {I} for our invariant, later adding the initialization steps needed to ensure that it holds on entering the loop for the first time. Notice that {I} is, in fact, a weaker version of the postcondition, i.e., when the postcondition is true, then so is the invariant. That was the inspiration for picking this particular invariant and designing the loop this way.
Now we need B. Remember that we need to have that {I Λ !B} => {Q}, or
{sum = 1 + 2 + ... + k-1 Λ !B} => {sum = 1 + 2 + ... + n}This logic falls neatly into place if we let !B be {k-1 = n}. So then B = !!B is simply
{!(k-1 = n)} => {k-1 != n} => {k != n+1}Let’s add the new information to our code outline:
{pre: _______}
[Initialization]
{inv: sum = 1 + 2 + ... + k-1}
while (k != n+1) {
{sum = 1 + 2 + ... + k-1}
sum = sum + k;
{sum = 1 + 2 + ... + k}
k = k+1;
{inv: sum = 1 + 2 + ... + k-1}
}
{sum = 1 + 2 + ... + k-1 Λ k = n+1} => {post: sum = 1 + 2 + ... + n}We’re almost there! We just need to initialize sum and k to values that will make the loop invariant true initially. One possible initialization is to set k=1 and sum to a value that establishes that sum is the sum of the elements in the set {1...k-1}. By convention, the set {i...j} for j < i is defined as the empty set, and the sum of an empty set is 0. Because k-1 = 0 < 1, we set sum to 0 to satisfy the invariant.
Finally, we just need the weakest precondition for the entire sequence of code. We need k <= n+1 initially or the loop will never terminate. Reasoning backwards, we arrive at the precondition n >= 0.
The complete code, with assertions, looks like this:
{pre: n >= 0}
sum = 0;
{n >= 0}
k = 1;
{inv: sum = 1 + 2 + ... + k-1}
{n+1 > 0 Λ sum = 1 + 2 + ... + k-1}
while (k != n+1) {
{inv: sum = 1 + 2 + ... + k-1}
sum = sum + k;
{sum = 1+2+...+k}
k = k+1;
{inv: sum = 1 + 2 + ... + k-1}
}
{sum = 1 + 2 + ... + k-1 Λ k = n+1} => {post: sum = 1 + 2 + ... + n}Example 2: Max
Write a loop to set max = largest value in items[0…size-1]
We get our postcondition directly from the problem:
{max = largest value in items[0...size-1]}A simple approach is to look through items one element at a time, keeping track of the largest value seen so far. The loop terminates when we’ve examined all elements. Much like in a typical for loop, we’ll keep a counter k, examining items[k] during each iteration of the loop and updating max if needed. From this description, the invariant {I} emerges naturally: {max = largest in items[0...k-1]}.
To choose {B}, recall that we want {I Λ !B} => {Q}, or
{max = largest in items[0..k-1] Λ !B} => {max = largest in items[0..size-1]}.This works if we set {!B} to {k = size}, or {B} = {k != size}.
Finally, we make {I} true initially by setting k = 1 and max = items[0]. This assumes the list is non- empty, so our precondition is size > 0.
Let’s put this all together:
{pre: size > 0}
k = 1 ;
max = items[0];
{inv: max = largest in items[0..k-1]}
while (k != size) {
{inv: max = largest in items[0..k-1]}
if (max < items[k]) {
{max = largest in items[0..k-1] Λ max < items[k]}
max = items[k];
{max = largest in items[0..k]}
else {
// nothing to do
{max = largest in items[0..k]}
}
k = k+1;
{inv: max = largest in items[0..k-1]}
}
{max = largest in items[0...k-1] Λ k = size} => {max = largest in items[0..size-1]}An aside: the code works, but only for non-empty lists (size > 0). What if the list is empty? We could treat that as an error, but we might like to accept the broadest set of inputs possible (i.e., make the precondition as weak as possible). One way we could do that is to return the result Int.min if size == 0. (Is this a good design decision? It depends on what properties we want to hold for this method.) We end up with something like:
// return largest value in list if not empty
// otherwise, return Int.min
func max() -> Int {
if (size == 0) {
return Int.min;
} else {
// code from above
}
}Example 3: Reverse
Given a[0…n-1], reverse the elements in a.
Choosing the invariant is a little subtler than for previous problems. We need to say something about the state of the whole array at each iteration. Let’s start with our precondition and postcondition to establish the initial and final state of the array:
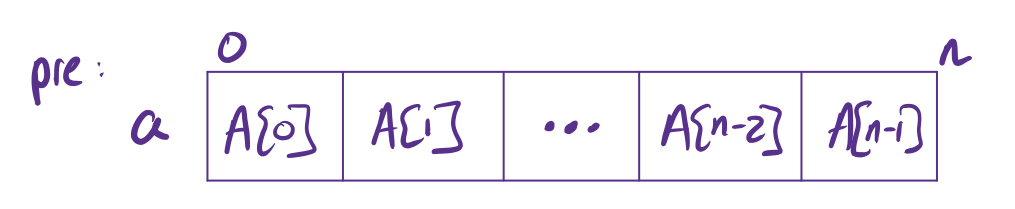

In our invariant, we will divide the array into three regions by weakening the postcondition: we have two regions at the front and back that have already been swapped and a region in the middle that still needs to be swapped.
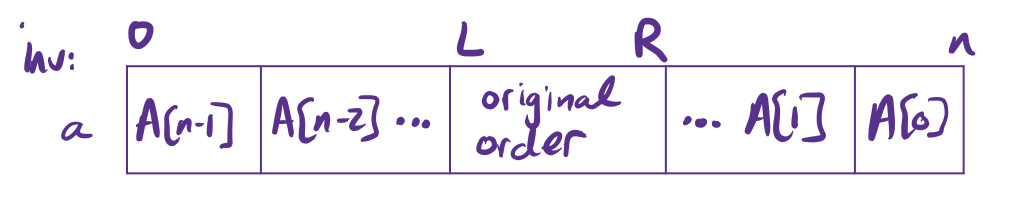
At each step of the loop, we will swap the items at the beginning and end of the unswapped section and adjust the endpoints. Let us define L and R as the first and last indices of the unswapped section, respectively. Alternatively, L could be the index just before the unswapped section and/or R could be the index just afterward. It doesn’t really matter which convention you use (though one might result in cleaner code) – just pick one and use it consistently! Bugs happen when someone forgets what they chose and writes part of the code assuming a different convention.
When the unswapped section only contains 0 or 1 elements, the entire list has been reversed. This occurs when L >= R, so {B} = {L < R}. Initially the entire list is unswapped, and we initialize L and R accordingly.
Putting it all together:
L = 0;
R = n-1;
while (L < R) {
swap(a[L],a[R]);
L = L+1;
R = R-1;
}To avoid extra detail and focus on reasoning about the loop, we assume we can write swap(x,y) to correctly interchange the values of variables x and y. We actually can’t easily write such a function in Swift, but it could easily be replaced with three assignment statements wherever it occurs if needed. (Making this replacement and proving it correct is left as an exercise for the reader.)
Example 4: Binary Search
Given a value x and sorted array a[0..n-1], find the index of x in a, if present. If x is not present, return an appropriate location in the array that can be used to insert x if desired.
The basic idea of binary search is to keep track of three regions of the array: a region at the front where all values are known to be <= x, a region at the end where all values are known to be > x, and an “unknown” region in the middle. At each iteration of the loop, we compare x to the element at the center of the unknown region and adjust the endpoints of the unknown region accordingly. We repeat this process until the unknown region is empty. Then x will be located or can be inserted at the end of the first region.
We will use L and R to represent the indexes immediately before and after the unknown region. Notice that this is a different convention than we used in the previous example, where L and R were the first and last elements of the middle region. Again, it doesn’t matter which convention we use as long as we are consistent, except that the one choice might make the code simpler or easier to follow than the other.
Our precondition is that the loop is already sorted:
pre: a[0] <= a[1] <= ... <= a[n-1]Our invariant shows what we know about the array at each step along the way, and our postcondition shows what we know at the end:
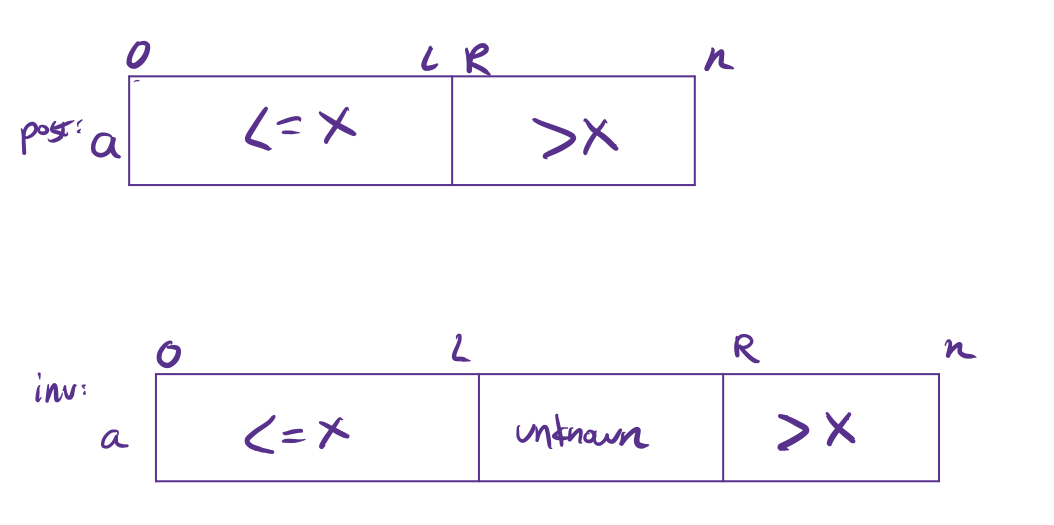
We can also write our invariant as:
inv: a[0..L] <= x Λ a[R..n-1] > x Λ a[L+1..R-1] unknownThe loop terminates when the unknown region is empty, i.e. L+1 = R. Initially the entire list is unknown, and we initialize L and R accordingly.
Putting it all together:
L = -1;
R = n;
while (L+1 != R) {
mid = (L+R)/2;
if (a[mid] <= x) {
L = mid;
} else {
// a[mid] > x
R = mid;
}
}
// x is found if L >= 0 && a[L] = x (note that the short-circuit
// property of && is essential here)As in the previous example, we glossed over proving the body of the loop in detail.
A note about termination
Some loops should run forever, for example a web server, but most of the loops we write should normally terminate. So a full proof that a loop is correct involves showing that it terminates as well as that it computes the right result. In fact, Hoare logic only says that if a loop terminates then the postcondition holds. We have ignored termination above to focus on the correctness issues.
There are various ways to prove termination, but a common strategy is the following:
- Map the state of the computation to a natural number somehow (only used “in the proof”)
- Prove that the natural number decreases on every iteration
- Prove that the loop test is false by the time the natural number gets to 0, if not sooner
For many of our examples, the appropriate number is the size of the unprocessed input:
- The quantity n - k in when we sum the numbers from 1 to n
- The size of the part of the array that has not yet been examined in the “find the max” and binary search problems
- The size of the unprocessed part of the array in the Dutch National Flag problem
In all of these cases the number decreases by 1 or more (for binary search) on each iteration of the loop.
Eventually the number reaches 0 and the loop must terminate at that point.