Hitori Strategy
Hitori puzzles involve coloring the squares of a numbered grid white or black. The puzzle is solved when
- All cells are white or black.
- Values in white cells are unique within each row or column.
The partial solution shown here:

fails because there are two 8's on the second row. - Black cells share no edges.
Here we see the 5 and 8 squares share an edge:
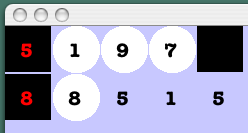
so at least one will be white. - White cells form a single mass connected along edges.
In the following solution, we see the 5 square can't reach any other white square (including the 9):

so at least one of the two black squares must be white.
Solving hitori puzzles does not involve guessing or backtracking.
My puzzles have unique solutions.
The 'Sandwich' Heuristic
When you see two equal values sandwich a third, the middle must be white:
Since the two outer values are equal, at least one will be black. Since two black cells cannot share an edge, the middle value must be white.
The 'Uniqueness' Rule
A white value forces all other equal values to black in the row and column: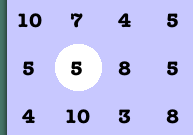
In this situation, the two uncommitted 5's in the middle row must be black.
The 'Odd-Man Out' Heuristic
When two adjacent values are equal, all other equal values in that row or column must be black:
Here, the rightmost 7 must be black, because one of the pair on the left must be white. A special form of this rule is when three equal values appear in a row:

Each of the outside values must be black, and the inside is forced to be white.
The Corner Heuristic
When three equal values go around a corner, the corner value must be black:
If the corner value had been white, the other edge values would be black, violating the white-connectedness rule.
The White-Connectedness Rule
Frequently squares must be white because if they were not, the remaining white squares would be broken into two or more components. A common example is the following pattern that appears frequently in a puzzle:
The 9 square should be colored white because if it were black, the 5 square would be isolated.
In the following situation,

all of the uncolored squares should be white. You should be able to convince yourself that coloring any of the squares black would force a separation of white components.
A Typical Solution
Here is a typical puzzle solution:
It is important to remember that every square is colored white or black for a good reason. The hardest part of hitori is recognizing the white squares that are forced because of the connectedness rule.