CS 136 - Lecture 31

  1. Dijkstra's Algorithm

Dijkstra's Algorithm

Dijkstra's Algorithm is a procedure to find shortest paths from a given vertex s in a graph G to all other vertices. The algorithm incrementally builds a sub-graph of G which is a tree containing shortest paths from s to every other vertex in the tree. A step of the algorithm consists of determining which vertex to add to the tree next.

Basic structures needed:

  1. The graph to be analysed. Denote it by G = (V,E), where V is the vertex set and E is the edge set.
  2. The tree T which is incrementally built, which can also be stored as a graph. Denote it by T = (S,A), where S is the vertex set and A is the edge set. Note that T is a subgraph of G.
  3. A priority queue in which each element is an edge (u,v) where u is in S and v is in V - S. The edge (u,v) has an associated value equal to the length of (u,v) plus the length of the path from s to u in T.
The algorithm proceeds as follows: 
T is the empty graph;
PQ is an empty priority queue;
Add s to T; mark s as visited in G;
Add each edge (s,v) of G to PQ with appropriate value
while (T.size() < G.size() and PQ not empty)
       do
           nextEdge = PQ.removeMin();
       until(one vertex of nextEdge is visited and the other is unvisited)
          or until there are no more edges in PQ

       // assume nextEdge = (v,u) where v is visited (in T) and u is
          unvisited (not in T)

       Add u to T; mark u as visited in G;
       Add (u,v) to T;
       for each unvisited neighbor w of u
          add (u,w) to PQ with appropriate weight
When the procedure finishes, T should contain all vertices reachable from s, along with a shortest path from s to each such vertex.

Disclaimer: Many details still need to be considered, but this is the essential information needed to implement the algorithm.

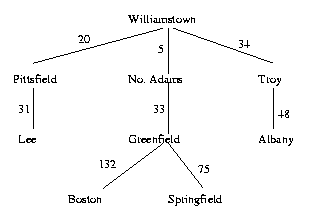
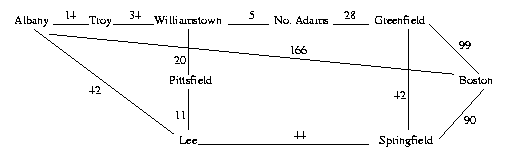
Consider the following graph:

From that graph, the algorithm would construct the following tree for a start node of Williamstown. Costs on edges indicate total cost from the root.