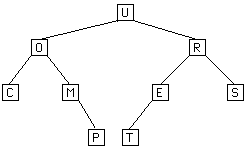
The array, data[0..n-1], holds the values to be stored in the tree. It does not contain references to the left or right subtrees.
Instead the children of node i are stored in positions 2*i +1 and 2*i + 2, and therefore the parent of a node j, may be found at (j-1)/2
The following example shows how a binary tree would be stored.

IndexRange: 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
data[]: U O R C M E S - - - P T - - -
Save space for links, but it is possible that there is exponentially much wasted storage:
Storing a tree of height n requires an array of length 2(n+1) - 1 (!), even if the tree only has O(n) elements. This makes this representation very expensive if you have a long, skinny tree. However it is very efficient for holding full or complete trees.
Def: A Min-Heap H is a complete binary tree such that
1) H is empty or
2a) The root value is the smallest value in H and
2b) The left and right subtrees of H are also heaps.
This is equivalent to saying that H[i] <= H[2*i+1], H[2*i+2] for all approp values of i in the array representation of trees. Another way of looking at Min-Heap is that any path from a leaf to the root is in non-ascending order.
This turns out to be exactly what is needed to implement a priority queue.
A priority queue is a queue in which the elements with
lowest priority values are removed before elements with higher priority.
public interface PriorityQueue {
public Comparable peek();
// pre: !isEmpty()
// post: returns the minimum value in priority queue
public Comparable remove();
// pre: !isEmpty()
// post: returns and removes minimum value from queue
public void add(Comparable value);
// pre: value is non-null comparable
// post: value is added to priority queue
public boolean isEmpty();
// post: returns true iff no elements are in queue
public int size();
// post: returns number of elements within queue
public void clear();
// post: removes all elements from queue
}
One can implement a priority queue as a regular queue where
either you work harder to insert or to remove an element (i.e. store in
priority order, or search each time to remove lowest priority elements).
Unfortunately, in these cases either adding or deleting an element will be O(n). (Which one is O(n) depends on which of the two schemes is adopted!)
Can provide more efficient implementation with heap!
- remove element with lowest priority (at root of
tree) and then remake heap.
public class VectorHeap implements PriorityQueue
{
protected Vector data;
public VectorHeap()
// post: constructs a new priority queue.
{
data = new Vector();
}
protected static int parentOf(int i)
// post: returns index of parent of value at i
{
return (i-1)/2;
}
protected static int leftChildOf(int i)
// post: returns index of left child of value at i
{
return 2*i+1;
}
protected static int rightChildOf(int i)
// post: returns index of right child of value at i
{
return 2*(i+1);
}
public Comparable peek()
// pre: !isEmpty()
// post: returns minimum value in queue
{
return (Comparable)data.elementAt(0);
}
public Comparable remove()
// pre: !isEmpty()
// post: removes and returns minimum value in queue
{
Comparable minVal = peek();
data.setElementAt(data.elementAt(data.size()-1),0);
data.setSize(data.size()-1);
if (data.size() > 1) pushDownRoot(0);
return minVal;
}
public void add(Comparable value)
// pre: value is non-null comparable object
// post: adds value to priority queue
{
data.addElement(value);
percolateUp(data.size()-1);
}
public boolean isEmpty()
// post: returns true iff queue has no values
{
return data.size() == 0;
}
protected void percolateUp(int leaf)
// pre: 0 <= leaf < size
// post: takes value at leaf in near-heap,
// and pushes up to correct location
{
int parent = parentOf(leaf);
Comparable value = (Comparable)(data.elementAt(leaf));
while (leaf > 0 && (value.lessThan((Comparable)(data.elementAt(parent)))))
{
data.setElementAt(data.elementAt(parent),leaf);
leaf = parent;
parent = parentOf(leaf);
}
data.setElementAt(value,leaf);
}
protected void pushDownRoot(int root)
// pre: 0 <= root < size
// post: pushes root down into near-heap
// constructing heap
{
int heapSize = data.size();
Comparable value = (Comparable)data.elementAt(root);
while (root < heapSize) {
int childpos = leftChildOf(root);
if (childpos < heapSize)
{
if ((rightChildOf(root) < heapSize) &&
(((Comparable)(data.elementAt(childpos+1))).lessThan
((Comparable)(data.elementAt(childpos)))))
{
childpos++;
}
// Assert: childpos indexes smaller of two children
if (((Comparable)(data.elementAt(childpos))).lessThan(value))
{
data.setElementAt(data.elementAt(childpos),root);
root = childpos; // keep moving down
} else { // found right location
data.setElementAt(value,root);
return;
}
} else { // at a leaf! insert and halt
data.setElementAt(value,root);
return;
}
}
}
...
}
Notice how these heap operations implement a priority queue.
When you add a new element in a priority queue, copy it into the next free position of the heap and sift it up into its proper position.
When you remove the next element from the priority queue,
remove the element from the root of heap (first elt, since it has lowest
number for priority), move the last element up to the first slot, and then
sift it down.
How expensive are sift up and sift down?
Each are log n. This compares very favorably with holding the priority queue as regular queue and inserting new elements into the right position in the queue and removing them from the front.