1. State Space Search
    1. An Example
    2. Search Strategies
      1. Breadth-first Search
      2. Depth-first Search
    3. Issues
      1. Evaluating breadth-first search
      2. Evaluating depth-first search
    4. Additional problems
    5. Terminology

Search

In considering robotic path planning, we discussed the method of state space search and, in particular, breadth-first search (BFS). State space search is a technique that can be applied to do problem solving more generally.

In AI, our goal is to create systems that handle particular applications, but we're also interested in finding solutions that are general enough for many applications.

To build a problem-solving system (agent), we need to:

  1. Define the problem precisely. Where do we start out? What's an acceptable solution?
  2. Represent the task knowledge that is necessary to solve the problem.
  3. Choose the best problem-solving technique(s).

The idea behind state space search as a technique is this: We note that our world is in a particular state (in which the problem is unsolved) that we wish to transform into another state (in which the problem is solved). We will consider all possible ways that the current state of the world can be changed. If any of these leads to the desired state, then we'll adopt that sequence of changes as our solution.

*Many (if not all) of the example applications we will look at are games/puzzles. why?

  1. because puzzle solving is clearly an example of problem solving
  2. because puzzles are interesting
  3. because they're well-defined!
  4. because they can be quite hard
  5. because it's hard to make a clear distinction between real and toy problems

A classic example. 8 puzzle

The 8 puzzle is a sliding tile puzzle. The task is to find a way to get from some initial configuration, such as

1

2

3
 

8

7

6

5

4

 

to a specific goal configuration, such as

1

2

3

4

5

6

7

8

  

 

 

Each possible puzzle configuration is a state

Operators transform one state to another

Through search we hope to find a sequence of operators that transforms the start state (initial state) to a state that meets the criteria for being a goal, i.e., that satisfies a goal test.

An example in more detail: the 5 puzzle

Let’s consider a simpler version of the 8 puzzle: the 5 puzzle.

To formulate this problem as a state space search problem, we need to specify:

For the 5 puzzle This formulation of the operators might seem unnatural. After all, you're used to thinking about moving the tiles. The advantage of this formulation is that it specifies all of the possible moves with only four simple options (rather than "move the 1, if it's possible; move the 2..."

Say that our start state (the initial configuration of the game) is
 

1

2

4

5

3

We will consider all possible moves that can be made in one step.

Then we will consider all possible moves that can be made in two steps.

And so on.

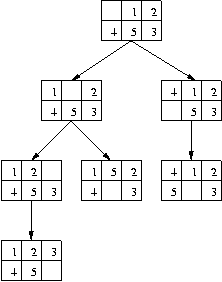
We do this until we reach the goal, as follows:

Now all we have to do is follow the path from the initial state to the goal. This gives us the sequence of moves that must be made in order to solve the puzzle!

Note that we aren’t solving the puzzle during the process of considering possible moves. As with robotic path planning, we use search to find the solution first and then execute the actual plan (path) later.

Search strategies

Recall that the style of search described above is Breadth-first Search (BFS).

We will consider this and three other search strategies in more detail.

Breadth-first search

Below is the BFS algorithm in a little more detail:

Begin at the initial state.

Do the following:

  1. Is the state that's currently under consideration a goal state?

    2. If so, then stop.

    Otherwise, generate the next steps that could be taken from here. i.e., apply the operators to the current state.

  2. If there's another state on the same level as the current state, go there next. Call that the current state.

    3. Otherwise, go to the first state on the next level.

  3. Go back to step 1.

Depth-first search

Begin at the initial state.

Do the following:

  1. Is the state that's currently under consideration a goal state?

    2. If so, then stop.

    Otherwise, generate the next steps that could be taken from here. i.e., apply the operators to the current state.

  2. If any next possible states were generated, visit one of those next. Call it the current state.

    3. Otherwise, go back up, and as soon as you encounter a state with a

    "child", visit that child.

  3. Go back to step 1.

Some issues

A number of issues arise in selecting and implementing search strategies. For example:

We will employ four criteria to evaluate and compare search strategies:

  1. Completeness: is the strategy guaranteed to find a solution when there is one?
  2. Optimality: does the strategy find the highest-quality solution?
  3. Time complexity: how long does it take to find a solution?
  4. Space complexity: how much computer memory is needed to perform the search?

Evaluating breadth-first search

BFS is complete and optimal.

We can evaluate the time complexity as follows: let b = the branching factor (i.e., the maximum number of next states from any given state),

and let d = length of solution.

Then the time it takes to find the solution is proportional to the number of states that must be explored to find it, i.e.,

1 + b + b2 + b3 + ... + bd

The space complexity is the same because you have to maintain the states that are being explored. In particular, you need to maintain the bottommost level in the search tree.

Evaluating depth-first search

DFS is neither complete nor optimal.

The time complexity is approximately bm, where m is the maximum depth of the search tree.

The space complexity, however, is much better. It is approximately mb, because only a single path needs to be stored at any given time.

Additional problems

Consider the following two problems. How would you go about finding solutions for them using state space search? In particular

Missionaries and Cannibals

Three missionaries and three cannibals find themselves on one side of a river. They have agreed that they would all like to get to the other side. But the missionaries are not sure what else the cannibals have agreed to. So the missionaries want to manage the trip across the river in such a way that the number of missionaries on either side of the river is never less than the number of cannibals who are on the same side. The only boat available holds only two people at a time. How can everyone get across the river without the missionaries risking being eaten?

[Text from Rich and Knight, Artificial Intelligence]

Eight Queens

The goal of the 8-queens problem is to place eight queens on a chessboard such that no queen attacks any other. (A queen attacks any piece in the same row, column or diagonal.)

[Text from Russell and Norvig, Artificial Intelligence: A Modern Approach]

Terminology